Cartes statistiques

Cartes statistiques#

Objectifs du cours#

Dans ce chapitre, il sera question de l’utilisation du modèle de régression pour générer des cartes statistiques cérébrales de groupe. Les statistiques de groupe permettent de combiner les mesures du cerveau de plusieurs individus et ainsi de contraster des groupes (ex. groupe de personnes jeunes et groupe de personnes âgées) ou bien de tester l’association avec une variable continue (ex. l’âge).

Les objectifs spécifiques du cours portent sur les concepts suivants :

la régression linéaire,
le modèle linéaire général,
tests statistiques.

Régression linéaire#

Variables#

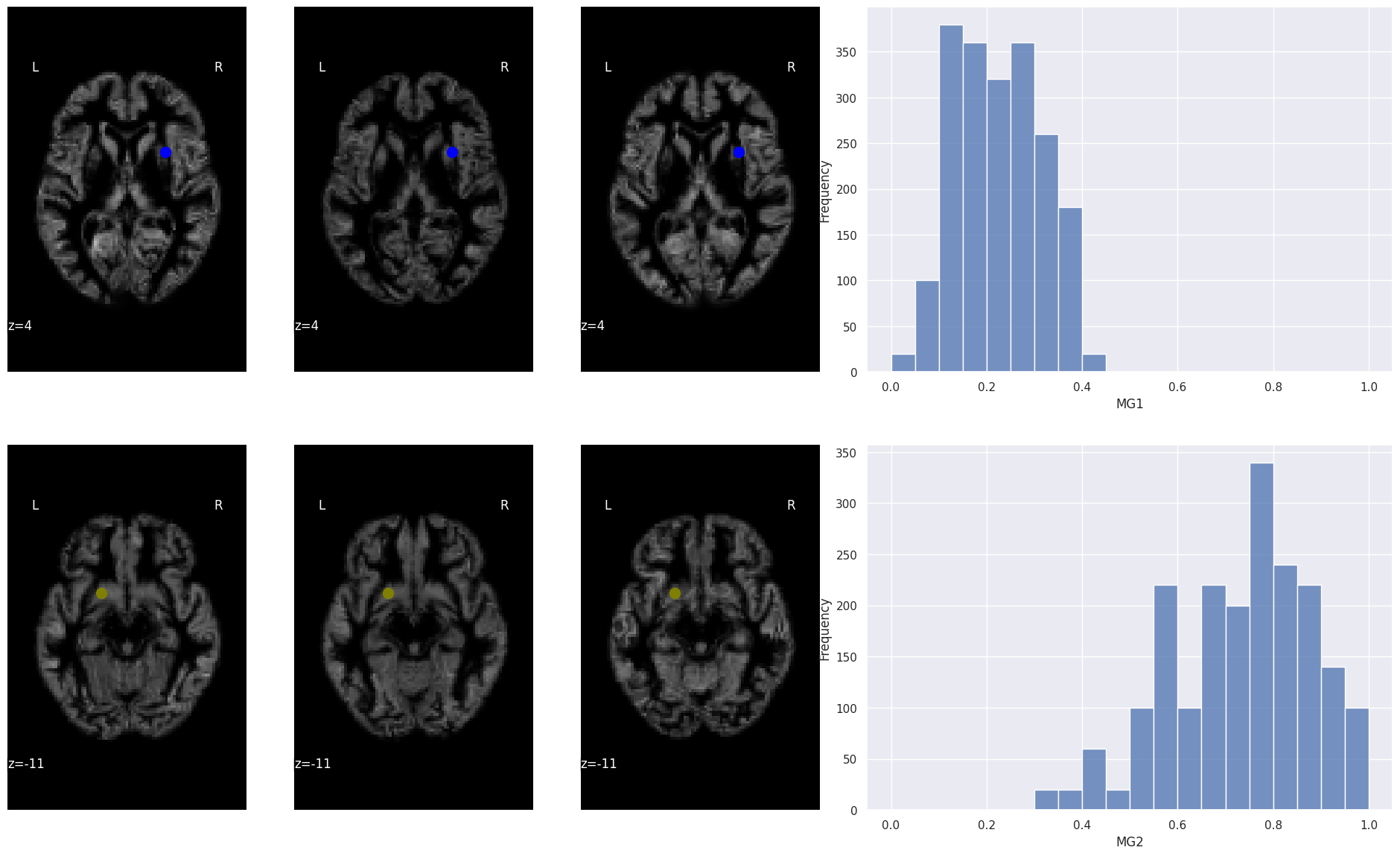
_images/dbaf0df29bc2eb8dbbf69df5bf94ebdcb6b41092a531b1f659f1ca2a80290bf9.png — Fig. 100 La position de deux voxels (illustrée à l’aide d’un cercle bleu (haut) et d’un cercle olive (bas)) est ici superposée sur des cartes de densité de matière grise pour différents sujets du jeu de données OASIS (Marcus et al., 2010). À droite, un histogramme représente la distribution de la densité de matière grise pour le voxel correspondant, à travers un échantillon de 100 sujets. Cette figure est adaptée d’un tutoriel de la librairie nilearn (cliquer sur + pour voir le code). Cette figure est distribuée sous licence CC-BY 4.0.#

Les concepts présentés dans ce chapitre s’appliquent à la plupart des modalités d’imagerie vues dans le cours de façon plus ou moins identique. Afin de rendre les choses un peu plus concrètes, nous allons ici nous intéresser à une analyse morphométrique de type VBM (IRM structurelle). Cette analyse utilise le jeu de données OASIS (Marcus et al., 2010). Des cartes de densité de matière grise pour les données OASIS sont disponibles via la librairie nilearn. Pour chaque voxel, on dispose d’une mesure locale de densité de matière grise qui varie entre 0 et 1. Comme toutes les images des 100 participants OASIS utilisés dans cet exemple ont été recalées dans un même espace stéréotaxique, chaque voxel est associé à une série de 100 mesures. Il s’agit de notre variable dépendante. On va par la suite chercher à expliquer les variations de cette mesure à travers les sujets à l’aide d’autres variables, appelées les prédicteurs. Pour notre exemple, nous allons démarrer avec l’âge des participants qui varie ici de 20 ans à 90 ans.

Modèle linéaire#

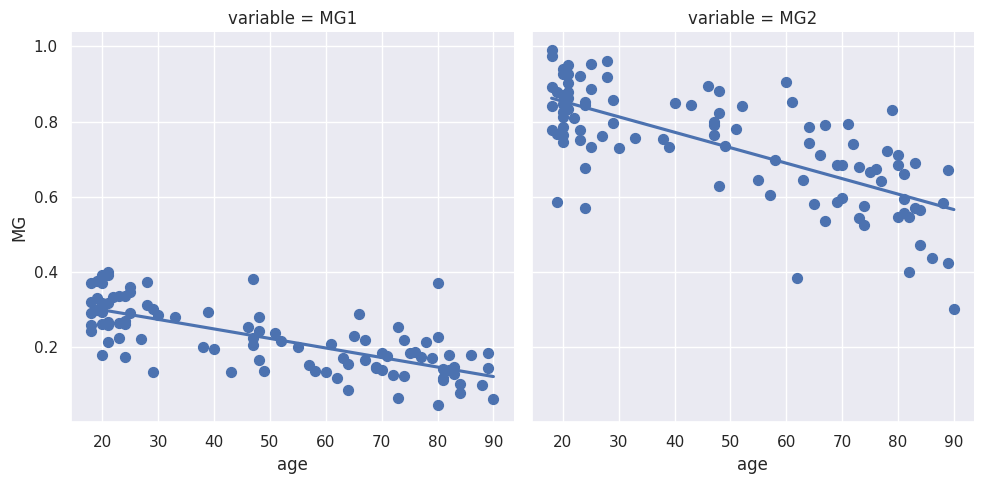
_images/c0223e79ee54ed01973a7abae12a22a7e9ab786990d92ad26534504cb18488e9.png — Fig. 101 Exemple de régression linéaire où la variable dépendante est la densité de matière grise pour un voxel et le prédicteur est l’âge. Les valeurs de densité de matière grise proviennent de 100 sujets de la base de données OASIS (Marcus et al., 2010). Les deux voxels utilisés ici sont les mêmes que ceux représentés dans la Fig. 100 (voxel bleu à gauche, voxel olive à droite). La régression linéaire est réalisée à l’aide de la libraire seaborn (cliquer sur + pour voir le code). Cette figure est distribuée sous licence CC-BY 4.0.#

Le concept soutenant le modèle de régression est une équation, ou une sorte de loi, qui va tenter de prédire la variable dépendante (ici, la densité de matière grise) à partir de prédicteurs (par exemple, l’âge). Mais contrairement à une loi physique qui tente de représenter une dépendance exacte (jusqu’à un certain degré), la présente loi ne capture qu’une fraction de la variance de notre mesure. La loi va donc incorporer un certain bruit représentant toutes les sources de variabilité que l’on ne peut pas capturer avec notre relation. La relation mathématique va prendre la forme suivante:

densite_matiere_grise = b0 + b1 * age + e

Où

densite_matiere_grise est la densité de matière grise mesurée pour un voxel
age est l’âge du participant de recherche
b0 est une valeur constante, appelée en anglais “intercept” (l’ordonnée à l’origine). Cette valeur est identique pour tous les sujets. Dans ce cas-ci, elle représenterait la densité de matière grise observée à la naissance (age=0), en moyenne sur la population.
b1 est une autre constante qui dans cet exemple mesure la réduction de matière grise par année de vie (en moyenne sur la population).
e est un bruit de mesure qui capture toutes les variations de densite_matiere_grise que l’on ne peut pas expliquer avec age. Typiquement, on suppose que la moyenne de e dans la population est 0 et que la variance de e est identique pour tous les sujets, égale à \(\sigma^2\).

On ne connaît évidemment pas les coefficients b0 et b1. Il sera nécessaire d’utiliser une procédure statistique pour les estimer, c’est-à-dire deviner (au mieux) leurs valeurs à partir des données dont nous disposons. Par exemple, pour la région de couleur olive (graphe de droite dans Fig. 101), on voit que l’on perd environ 25% de densité entre 20 ans et 90 ans (voir Fig. 101). On perd donc environ 0.35% de densité de matière grise par an, soit b1 ~ -0.0035. En utilisant cette valeur et en remarquant que la densité de matière grise est d’à peu près 0.85 à 20 ans, on en déduit que la densité à la naissance devrait être b0=0.92. En pratique, la procédure statistique va choisir les valeurs b0 et b1 pour minimiser l’amplitude des résidus de la régression:

residus = densite_matiere_grise - b0 - b1 * age

Une fois les coefficients b0 et b1 estimés, on peut tracer une droite qui représente les valeurs de densité de matière grise prédites à partir de l’âge des sujets (voir Fig. 101). Si le modèle permet d’expliquer une partie importante de la variabilité de la variable dépendante, les points mesurés seront proches de la droite de prédiction.

Analyse massivement univariée#

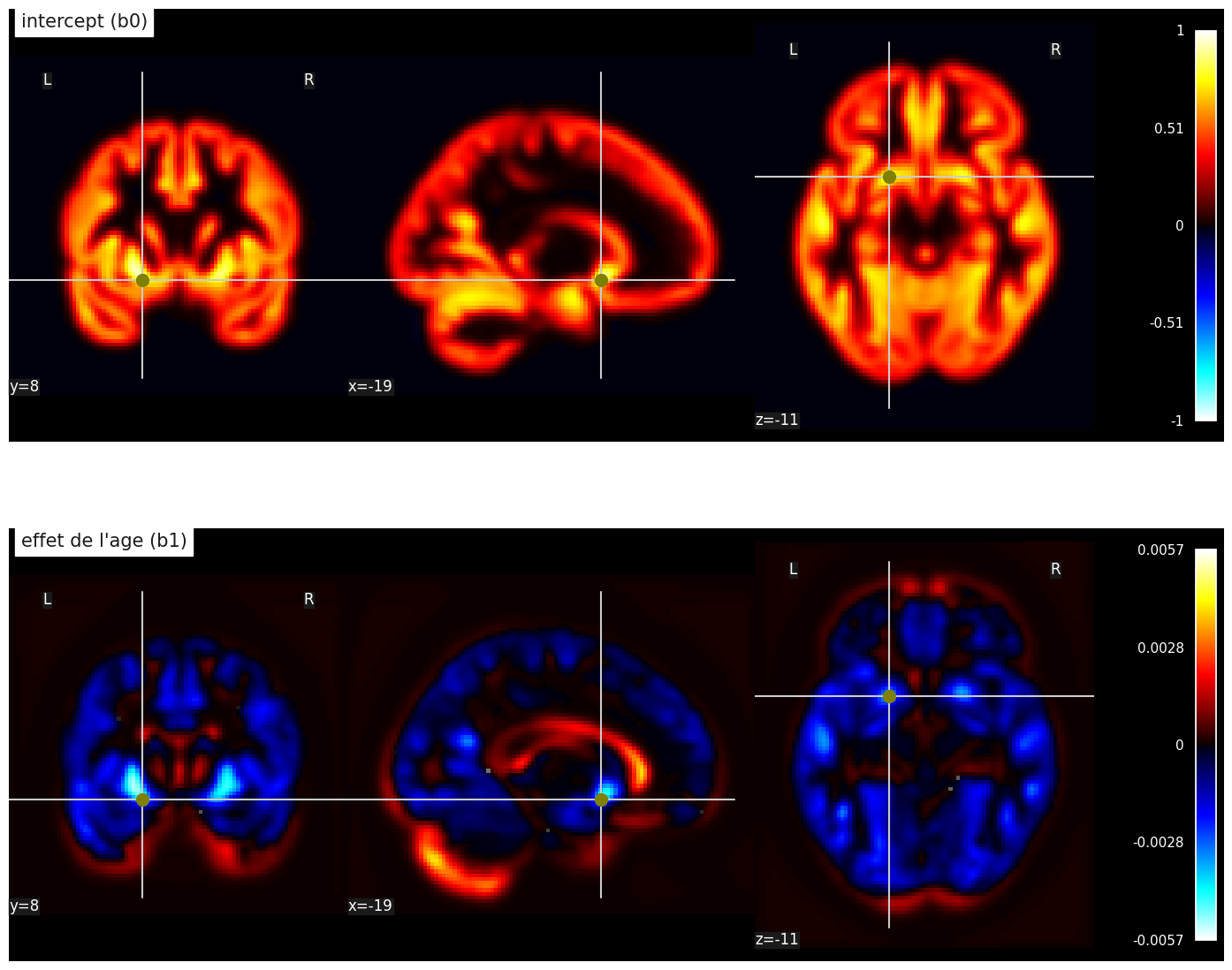
_images/1675b40e13425f6c85cf2e8b3854433d02a52e61864b5b8efb7960949ccd5459.png — Fig. 102 Cartes de paramètres statistiques dans une régression linéaire massivement univariée. Première ligne: intercept `b0`, deuxième ligne: effet linéaire de l’âge `b1`. Cette figure est adaptée d’un tutoriel de la librairie nilearn (cliquer sur + pour voir le code). Cette figure est distribuée sous licence CC-BY 4.0.#

Pour l’instant, nous avons utilisé un modèle de régression pour deux voxels seulement. Mais une carte VBM peut inclure des centaines de milliers de voxels. Les logiciels de neuroimagerie permettent d’effectuer systématiquement une régression linéaire pour l’ensemble des voxels, simultanément. Dans ce cas, on estime deux paramètres pour chaque voxel: b0 (l’intercept) et b1 (l’effet de l’âge). On va donc générer deux cartes statistiques séparées (voir Fig. 102). Ces deux cartes récapitulent donc des milliers de modèles de régression différents. Comme les régressions effectuées à chaque voxel sont indépendantes les unes des autres, on parle de modèle univarié. L’autre option, le modèle multivarié, chercherait plutôt à combiner les valeurs obtenues à différents voxels. De plus, comme on fait un très grand nombre de régressions en même temps, on parle de régression massivement univariée.

Statistiques et multimodalité

Le modèle de régression est appliqué à plusieurs modalités de neuroimagerie. Dans ce chapitre, il est question d’un exemple utilisant la VBM. Mais le même modèle fonctionne dès lors qu’on a une série de cartes pour différents sujets. Il pourrait par exemple être utilisé en IRMf ou bien en TEP. Le même type de modèle peut aussi s’appliquer à des mesures prises sur des récepteurs en imagerie optique ou des mesures moyennes sur un faisceau de fibres en IRMd. Le modèle de régression est partout!

Modèle linéaire général#

Variables#

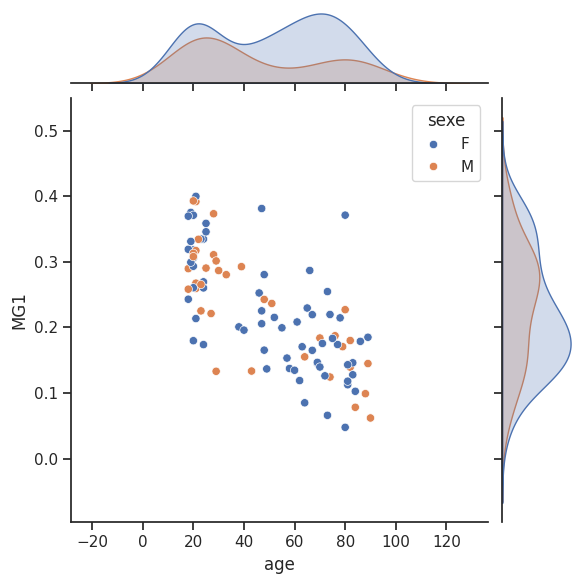
_images/066646da3bfe1a83ff3561f5e67a628b415b96296b117ef89532cb10b0934f25.png — Fig. 103 Relation entre âge, sexe et densité de matière grise pour un voxel (le voxel de couleur bleu dans Fig. 100). Le graphique est réalisé à l’aide de la libraire seaborn (cliquer sur + pour voir le code). Cette figure est distribuée sous licence CC-BY 4.0.#

L’approche de régression linéaire que l’on vient de voir est simple et puissante, mais elle est limitée à deux variables. En neurosciences humaines, on ne se trouvera généralement pas dans ce cas. On va très souvent vouloir étudier des facteurs multiples de manière conjointe. Même si la représentation du sexe des participants par une variable binaire est très (très) simplificatrice - sans compter la diversité de l’identité de genre - nous allons quand même essayer d’intégrer le sexe (mâle vs femelle) dans notre analyse. La figure ci-dessus montre les distributions d’âge et de matière grise (pour le voxel bleu), séparées par sexe. Ce graphique suggère que la distribution de matière grise est peut-être différente entre mâle et femelle, mais cette différence pourrait également être liée à l’âge. Le modèle linéaire général nous permet d’intégrer toutes ces variables dans une seule analyse.

Régression multiple#

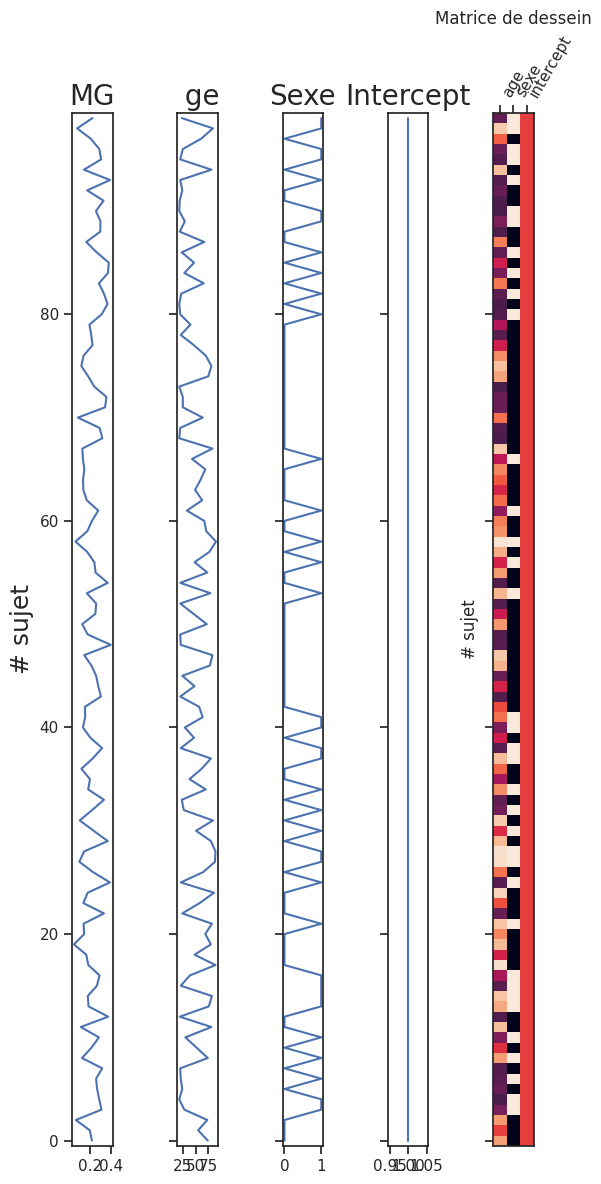
_images/92604a2988576a34207bff2299e7032e7452316ae96423db34bf024850832099.png — Fig. 104 Variables pour une régression multiple. La variable dépendante est la densité de matière grise pour un voxel (MG, le voxel de couleur bleu dans Fig. 100). Les autres colonnes représentent les variations de l’âge, du sexe et de l’intercept à travers les sujets (variables prédictives). Les variables prédictives sont généralement représentées de manière plus compacte, sous la forme d’une image où la couleur de chaque pixel représente l’intensité du régresseur. Le graphique est adapté d’un code python produit par l’équipe Dartbrains, ainsi que d’un tutoriel nilearn (cliquer sur + pour voir le code). Cette figure est distribuée sous licence CC-BY 4.0.#

D’un point de vue mathématique, le modèle de régression multiple, parfois appelé modèle linéaire général, consiste simplement à incorporer plus de variables dans la “loi” qui tente de prédire la variable dépendante à partir des régresseurs: densite_matiere_grise = b0 + b1 * age + b2 * sexe + e

Le seul nouveau coefficient est b2, qui dans ce cas mesure la différence entre la moyenne de matière grise entre les femelles (codées avec un 0 dans le modèle) et les mâles (codés avec un 1 dans le modèle), après un ajustement pour l’âge des sujets. Ce type de codage est utilisé avec les données catégorielles et est appelé “dummy variable” en anglais. Il permet d’intégrer des tests de différence de moyenne entre les groupes dans un modèle de régression.

Régression multiple et statistiques classiques

Le modèle de régression multiple est très flexible. Il est possible de formuler la plupart des tests statistiques classiques tels que l’analyse de variance (ANOVA) ou bien le test d’égalité des moyennes de Student (t-test) à l’aide du modèle de régression linéaire. Voir ce guide pour plus de détails.

Cartes statistiques#

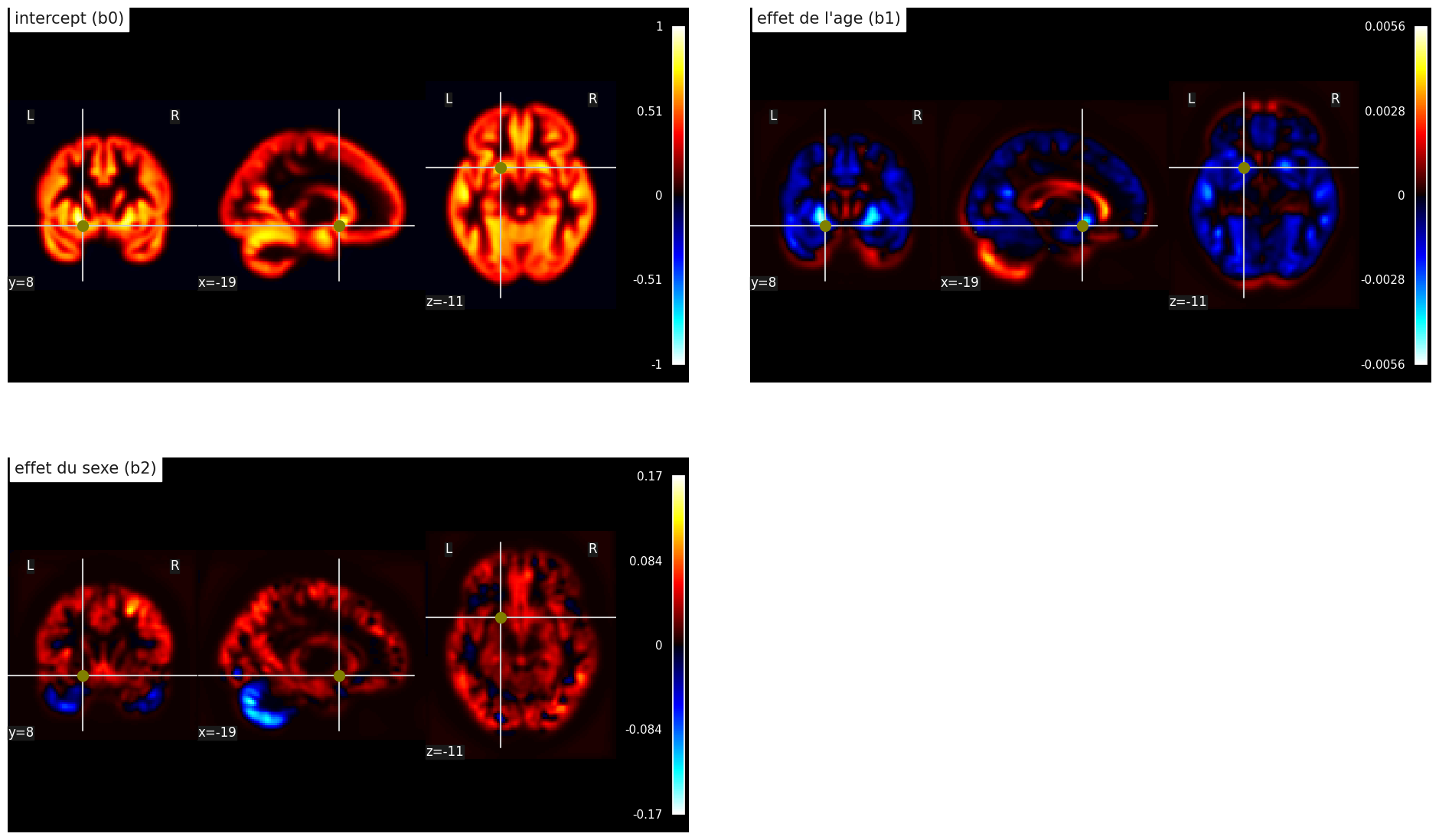
_images/88c3dace5c2436a5109dce96f5306538d934996f69d7715825b8802c72f7a763.png — Fig. 105 Cartes de paramètres statistiques dans une régression linéaire multiple massivement univariée. Haut gauche: intercept `b0`, haut droite: effet linéaire de l’âge `b1`, bas gauche: effet linéaire du sexe `b2`. Cette figure est adaptée d’un tutoriel de la librairie nilearn (cliquer sur + pour voir le code). Cette figure est distribuée sous licence CC-BY 4.0.#

Une caractéristique qui peut être légèrement contre-intuitive avec la régression multiple est que la carte présentant l’effet de l’âge ici est différente de celle présentée dans la section portant sur la régression simple. En effet, l’effet de l’âge est maintenant évalué après avoir pris en compte des différences de sexe. Malgré cela, le résultat de la régression n’a pas changé de manière frappante: le cortex s’atrophie avec l’âge (en bleu), alors que le liquide céphalo-rachidien s’étend (en rouge). Ce qui apparaît comme une expansion de la matière grise reflète probablement des effets de volume partiel et des tissus classifiés incorrectement comme de la matière grise. L’analyse sur la variable sexe montre que la densité de matière grise est plus élevée (en moyenne) dans le cortex chez les hommes, alors que la tendance est inversée au niveau du cervelet.

Tests statistiques#

Tests t et valeur p#

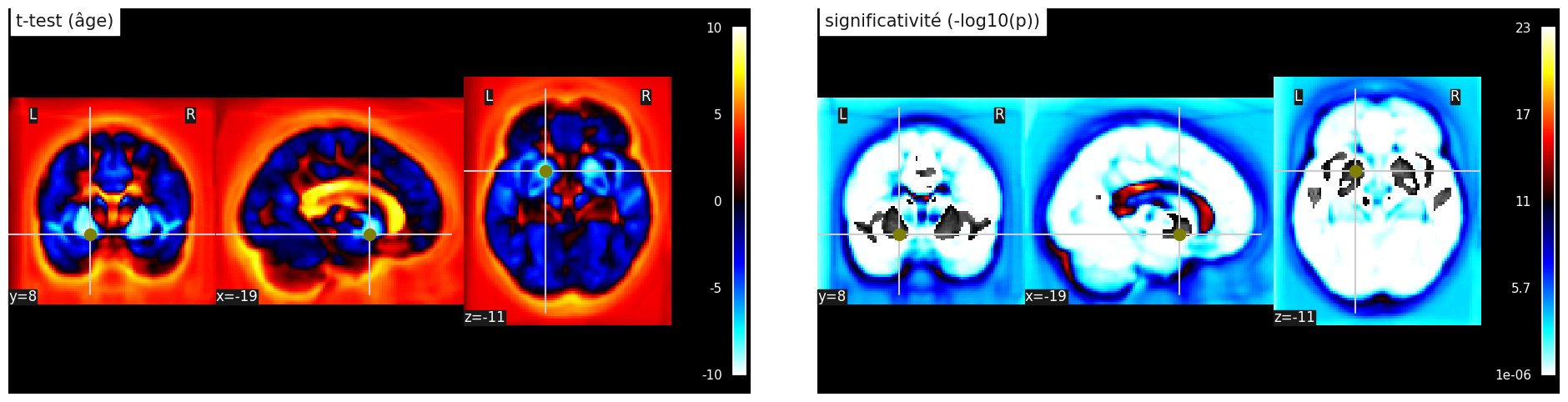
_images/8ebc4302f4849a5a7433ddad66f800774f7119d9775283f6f2348f89fc53f296.png — Fig. 106 Tests statistiques sur la significativité de l’association entre densité de matière grise et âge. Test t de Student (haut) et log10(p) (bas). Cette figure est adaptée d’un tutoriel de la librairie nilearn (cliquer sur + pour voir le code). Cette figure est distribuée sous licence CC-BY 4.0.#

Une fois que l’on a estimé l’effet de certaines variables explicatives (par exemple, l’âge) sur notre variable dépendante (par exemple, la densité de matière grise), il est nécessaire de tester la significativité de cet effet. À cette fin, on utilise l’amplitude des résidus pour estimer la taille d’effet que l’on pourrait observer par chance, si uniquement ces résidus étaient présents. On en déduit un test t de Student, qui se comporte comme une loi normale quand le nombre de sujets est grand. Pour chaque voxel, on a donc une statistique t différente, et on peut calculer la probabilité p d’observer cette statistique sous l’hypothèse nulle, où l’effet de la variable explicative est exactement zéro.

Hypothèse nulle#

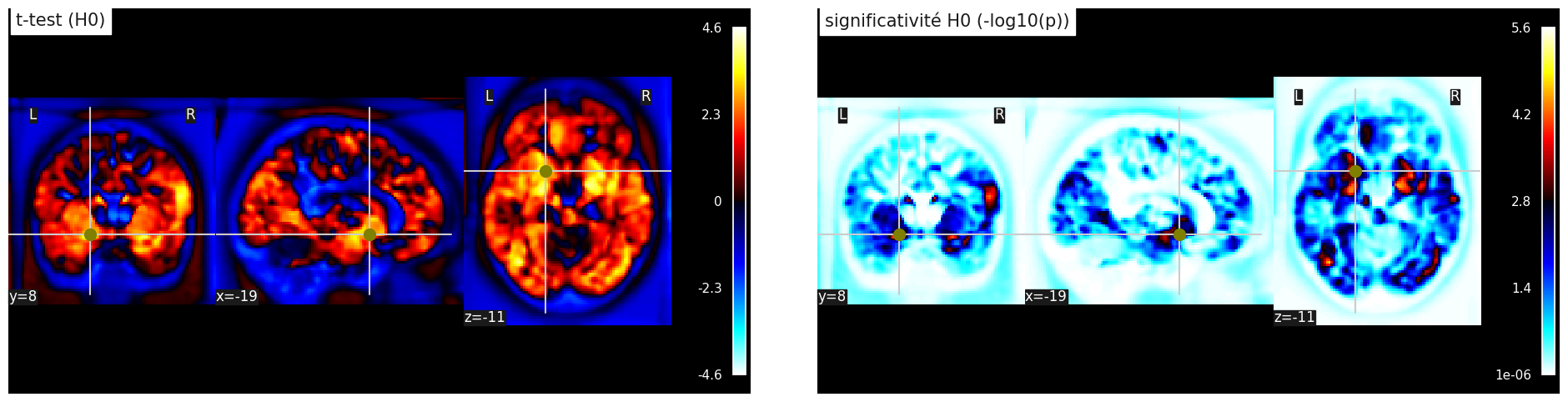
_images/a1fde922a9a52aee0762df5799b241bab850ec978fc19e957442bcd6210d9fe5.png — Fig. 107 Tests statistiques sur la significativité de l’association entre densité de matière grise et âge, sous l’hypothèse nulle où il n’existe aucune association. Les données d’âge ont été permutées aléatoirement entre les sujets. Test t de Student (haut) et log10(p) (bas). Cette figure est adaptée d’un tutoriel de la librairie nilearn (cliquer sur + pour voir le code). Cette figure est distribuée sous licence CC-BY 4.0.#

Au coeur de l’interprétation de la valeur p, il y a ce qu’on appelle l’hypothèse nulle. Pour essayer de comprendre ce que cela veut dire, faisons une expérience. Nous allons recommencer toute la procédure d’estimation de l’effet de l’âge sur la densité de matière grise. Mais cette fois ci, au lieu d’utiliser l’âge réel des sujets, nous allons mélanger ces valeurs aléatoirement (on parle de permutations). La distribution des tests t et des valeurs p est présentée dans la Fig. 107. De manière frappante, les valeurs t sont beaucoup plus petites avec les valeurs d’âge aléatoires que lorsqu’on a fait l’analyse avec les vraies valeurs, mais certaines valeurs restent élevées. On a réalisé une expérience sous l’hypothèse nulle, où il n’existe aucune association avec l’âge. La valeur p nous indique la fréquence avec laquelle on trouvera des valeurs d’effet de l’âge plus élevées sous l’hypothèse nulle que dans l’échantillon original. Pour estimer cela directement, il faudrait recommencer l’expérience que l’on vient de faire avec des milliers de permutations! Mais il existe aussi des méthodes approximées plus rapides.

Comparaisons multiples#

Show code cell source Hide code cell source

from nilearn.glm import threshold_stats_img
from scipy.stats import norm
p_val = 0.001
p001_uncorrected = norm.isf(p_val)
p_val = 0.05
p05_uncorrected = norm.isf(p_val)

# On génère la Figure
from nilearn import plotting
import seaborn as sns
fig = plt.figure(figsize=(24, 18))

ax = plt.subplot2grid((3, 4), (0, 2), colspan=2)
roi_img = plotting.plot_stat_map(
    z_score, threshold=p05_uncorrected, bg_img=gray_matter_map_filenames[0], cut_coords=coords[1], figure=fig,
    axes=ax, display_mode='ortho', colorbar=True, title='t-test, p<0.05')
roi_img.add_markers([coords[1]], colors[1], 100)

ax = plt.subplot2grid((3, 4), (1, 2), colspan=2)
roi_img = plotting.plot_stat_map(
    z_score, threshold=p001_uncorrected, bg_img=gray_matter_map_filenames[0], cut_coords=coords[1], figure=fig,
    axes=ax, display_mode='ortho', colorbar=True, title='t-test, p<0.001')
roi_img.add_markers([coords[1]], colors[1], 100)

ax = plt.subplot2grid((3, 4), (2, 2), colspan=2)
thresholded_map, threshold = threshold_stats_img(
    z_score, alpha=.05, height_control='bonferroni')
roi_img = plotting.plot_stat_map(
    z_score, threshold=threshold, bg_img=gray_matter_map_filenames[0], cut_coords=coords[1], figure=fig,
    axes=ax, display_mode='ortho', colorbar=True, title='t-test, p<0.05 corrigé')
roi_img.add_markers([coords[1]], colors[1], 100)

ax = plt.subplot2grid((3, 4), (0, 0), colspan=2)
roi_img = plotting.plot_stat_map(
    z_score_rand, threshold=p05_uncorrected, bg_img=gray_matter_map_filenames[0], cut_coords=coords[1], figure=fig,
    axes=ax, display_mode='ortho', colorbar=True, title='t-test (H0), p<0.05')
roi_img.add_markers([coords[1]], colors[1], 100)

ax = plt.subplot2grid((3, 4), (1, 0), colspan=2)
roi_img = plotting.plot_stat_map(
    z_score_rand, threshold=p001_uncorrected, bg_img=gray_matter_map_filenames[0], cut_coords=coords[1], figure=fig,
    axes=ax, display_mode='ortho', colorbar=True, title='t-test (H0), p<0.001')
roi_img.add_markers([coords[1]], colors[1], 100)

ax = plt.subplot2grid((3, 4), (2, 0), colspan=2)
thresholded_map_rand, threshold_rand = threshold_stats_img(
    z_score_rand, alpha=.05, height_control='bonferroni')
roi_img = plotting.plot_stat_map(
    z_score_rand, threshold=threshold_rand, bg_img=gray_matter_map_filenames[0], cut_coords=coords[1], figure=fig,
    axes=ax, display_mode='ortho', colorbar=True, title='t-test (H0), p<0.05 corrigé')
roi_img.add_markers([coords[1]], colors[1], 100)

# On colle la figure dans le jupyter book
from myst_nb import glue
glue("threshold-fig", fig, display=False)           

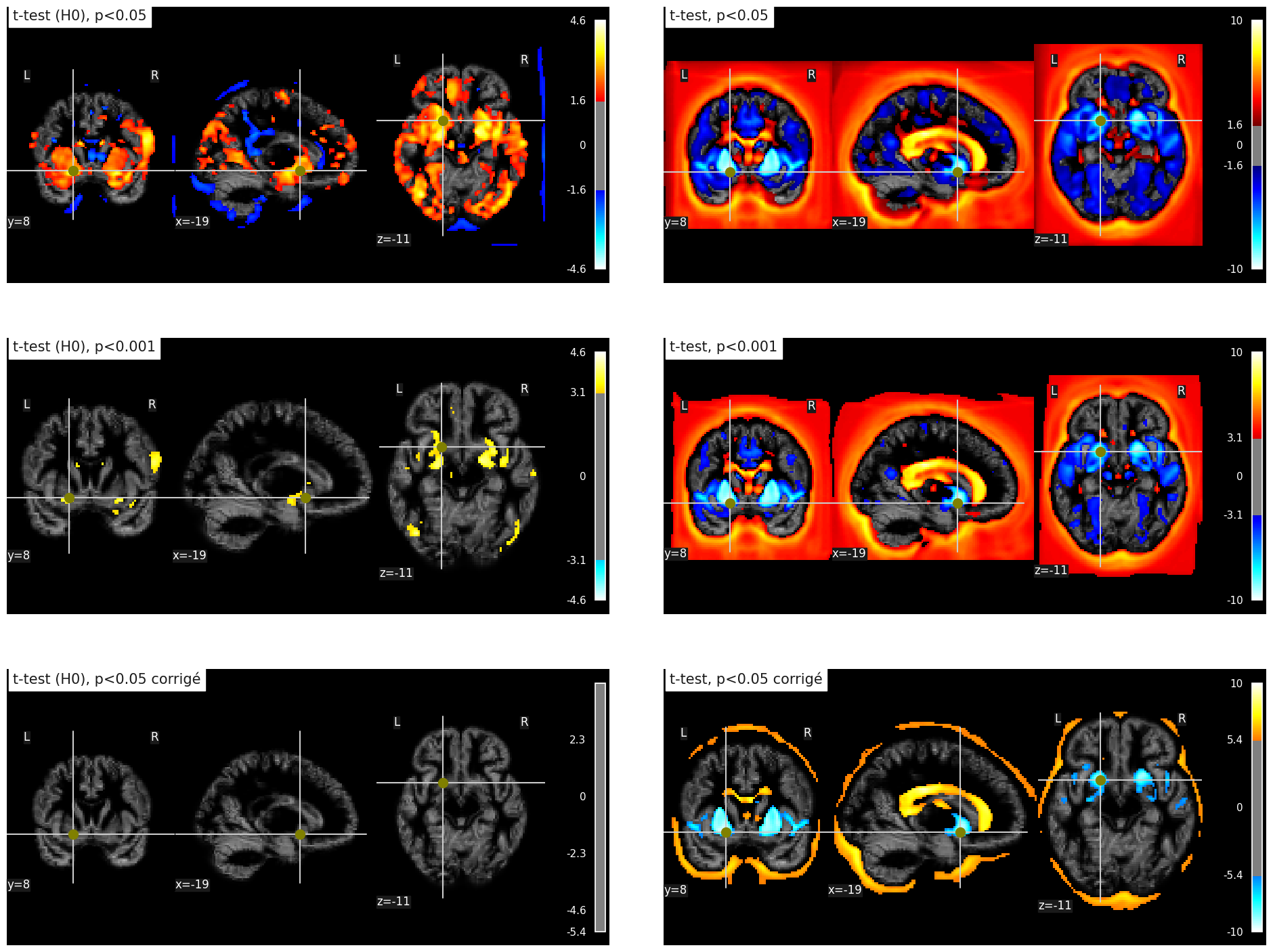
_images/95c4ab9fa4057cad14ef6c81f60786d449d4d2f45deb269cf22cfbf9d638a31f.png — Fig. 108 Effet de différentes stratégies de seuillage sur l’association entre l’âge et la densité de matière grise. À gauche: données sous l’hypothèse nulle (valeurs d’âge permutées au travers des sujets). À droite: données originales. Ligne 1: seuil `p<0.05` non corrigé pour les comparaisons multiples; ligne 2: seuil `p<0.001` non corrigé pour les comparaisons multiples; seuil `p<0.05` corrigé pour les comparaisons multiples par l’approche de Bonferroni. Cette figure est adaptée d’un tutoriel de la librairie nilearn (cliquer sur + pour voir le code). Cette figure est distribuée sous licence CC-BY 4.0.#

Maintenant que l’on a discuté de l’interprétation de la valeur p, on doit maintenant décider d’un seuil à appliquer sur les valeurs p. Si l’on utilise le seuil habituel p<0.05, cela signifie que pour 20 permutations, on détectera une association 1 fois (en moyenne) pour un voxel donné. Mais comme on a des milliers de voxels dans le cerveau, cela veut dire que l’on va détecter 5% du cerveau (en moyenne) pour chaque permutation! C’est ce que l’on observe (et même plus) dans la figure en haut à gauche Fig. 108. Il s’agit du problème de comparaisons multiples, et plus on fait de tests, plus ce problème est important.

Si l’on abaisse le seuil à p<0.001, on ne détecte plus que 0.1% du cerveau (en moyenne) sous l’hypothèse nulle, et on observe en effet une réduction du nombre de voxels dans la figure de gauche, 2ième ligne Fig. 108.

La méthode la plus simple pour corriger du problème de comparaisons multiples est d’utiliser un seuil corrigé p<0.05/N, où N est le nombre de comparaisons (c’est-à-dire de tests). Dans notre cas, on a approximativement 100,000 voxels, donc on va utiliser p<0.0000001! Avec cette stratégie, aucun voxel ne passe le seuil dans notre expérience sous l’hypothèse nulle, voir figure en bas à gauche Fig. 108. En général, c’est ce qui se passe (en moyenne) pour 19/20 permutations.

Si l’on observe maintenant l’effet de ces différentes stratégies sur les données originales, on observe que plus le seuil p est petit, moins on détecte d’effets significatifs. Malgré tout, même avec p<0.05 corrigé par l’approche de Bonferroni, on détecte toujours les effets principaux de l’âge.

Compromis résolution / puissance

En règle générale, on doit faire un compromis entre la résolution (notre capacité à détecter des effets dans de petites régions du cerveau) et la puissance statistique (notre capacité à détecter des effets de petite taille). Si l’on veut une excellente résolution, on fait des tests à tous les voxels, mais on doit corriger pour un très grand nombre de comparaisons multiples. En revanche, si l’on ne teste qu’une valeur moyenne sur une région, on n’a qu’un seul test et aucune correction à appliquer, mais on ne sait pas ce qui se passe dans le reste du cerveau, ou à l’intérieur de cette région.

Conclusion#

Le modèle de régression simple permet de prédire les observations d’une variable dépendante à partir d’une variable explicative.
Ce modèle est appliqué indépendamment à chaque voxel (approche massivement multivariée).
Il est possible d’utiliser le modèle linéaire général pour tester simultanément l’effet de plusieurs variables explicatives sur la variable dépendante.
Quand on effectue un grand nombre de tests statistiques à chaque voxel, il faut modifier le seuil de significativité du test (problème de comparaisons multiples).

Exercices#

Exercice 1

Vrai/faux. Le modèle de régression général peut être utilisé pour effectuer des statistiques de groupe pour les types de mesures suivantes…

IRMf
IRM T1 (VBM)
IRM T1 (volumétrie)
IRM T1 (épaisseur corticale)
Tomographie par émission de positrons
Imagerie optique
Imagerie de diffusion

Exercice 2

Vrai/faux. La situation suivante inclut un problème de comparaisons multiples en statistique:

On effectue de manière répétée des mesures du volume cérébral chez N=100 sujets jeunes et N=100 sujets âgés, puis on compare statistiquement la moyenne des deux groupes.
On répète un test statistique à chaque voxel dans une image du cerveau, par exemple.
On acquiert 300 volumes cérébraux chez un individu en IRMf.
On a quatre sous-groupes, et on compare statistiquement chacune des trois paires possibles de sous-groupes, par exemple.

Exercice 3

Choisissez la bonne réponse. On observe une différence de moyenne entre deux groupes, et l’on effectue un test statistique qui nous donne une valeur p.

La valeur p est la probabilité de l’hypothèse nulle où il n’existe pas de vraie différence.
Une faible valeur p indique une forte probabilité qu’il y ait une vraie différence.
La valeur p indique la probabilité d’observer cette différence, au moins, s’il n’existait vraiment aucune différence entre les deux groupes.

Exercice 4

On considère les analyses suivantes: (hippocampe) On compare le volume de l’hippocampe entre deux groupes de sujets.

(VBM) On compare la densité de matière grise entre deux groupes de sujets à chaque voxel du cerveau.
(atlas) On compare le volume de régions cérébrales entre deux groupes de sujets, à partir d’un atlas qui comprend 90 régions.
(FDG) On compare le métabolisme du glucose entre deux groupes de sujets à chaque voxel du cerveau, à l’aide du FDG-TEP.

On classe les analyses en fonction du nombre de comparaisons multiples impliquées. Choisissez la bonne réponse:

VBM > atlas
atlas > hippocampe
atlas > FDG
Réponses 1 et 2.
Réponses 1, 2 et 3.

Exercice 5

On souhaite comparer la connectivité au repos en IRMf à partir d’une région cible dans le cortex cingulaire postérieur entre deux groupes de sujets, jeunes vs âgés. On applique un modèle linéaire général à chaque voxel.

Décrivez les variables prédictives indispensables à inclure dans ce modèle.
Quelles autres variables vous semblent-elles importantes à inclure dans le modèle?
Est-ce que ces variables peuvent modifier la différence observée entre personnes jeunes et âgées?

Exercice 6

Pour répondre aux questions de cet exercice, lisez d’abord l’article Tau pathology in cognitively normal older adults de Ziontz et collaborateurs (disponible comme preprint sur Biorxiv sous licence CC0). Les questions suivantes requièrent des réponses à développement court.

Quelle est la variable dépendante du modèle linéaire?
Quelles variables explicatives sont incluses dans le modèle linéaire?
Sait on combien de comparaisons multiples sont faites?
Comment est-ce que les comparaisons multiples sont corrigées?

Cartes statistiques

Contents

Cartes statistiques#

Objectifs du cours#

Régression linéaire#

Variables#

Modèle linéaire#

Analyse massivement univariée#

Modèle linéaire général#

Variables#

Régression multiple#

Cartes statistiques#

Tests statistiques#

Tests t et valeur p#

Hypothèse nulle#

Comparaisons multiples#

Conclusion#

Exercices#