IRM de diffusion

IRM de diffusion#

Objectifs du cours#

Ce cours a pour but de vous initier aux principes de l’imagerie par résonance magnétique de diffusion (IRMd). L’IRMd est une modalité de neuroimagerie qui nous permet d’étudier les fibres de matière blanche. Nous allons donc pouvoir examiner les connexions entre différentes régions, autant interhémisphériques (i.e., fibres de matière blanche voyageant d’un hémisphère à l’autre), qu’intrahémisphériques (i.e., fibres de matière blanche voyageant au sein d’un même hémisphère). Pour vous faire une idée concrète de ce à quoi ressemblent les fibres de matière blanche, vous pouvez regarder cette vidéo présentant des dissections cérébrales, tirée du cours de neuroanatomie fonctionnelle de UBC.

Pendant ce cours, nous allons aborder :

Les principes physiques et physiologiques du signal en IRMd.
Le modèle du tenseur de diffusion.
Les analyses de tractographie.

Principes physiques et physiologiques#

Diffusion de l’eau#

_images/diffusion-water.jpg — Fig. 64 Illustration de la diffusion d’une goutte d’encre dans un verre d’eau. Image par Narudon Atsawalarpsakun disponible sur shutterstock ID `736860766`, utilisée sous licence shutterstock standard.#

En IRM de diffusion, nous nous intéressons à la manière dont l’eau diffuse dans le cerveau. En examinant comment l’eau se diffuse, nous pouvons apprendre des informations sur le milieu de diffusion, dans notre cas, le cerveau ! Plus précisément, l’IRMd nous permet d’en apprendre davantage sur les propriétés de la microstructure des fibres de matière blanche. Pour un exemple concret de diffusion, nous pouvons imaginer ce qui se passe lorsque nous laissons tomber une goutte d’encre dans un verre d’eau, illustrée en Fig. 64. L’encre va au cours du temps se diffuser dans l’eau, colorant l’eau petit à petit, jusqu’à ce qu’elle devienne colorée de manière homogène. Les molécules d’eau et d’encre entrent en collision dans des directions aléatoires, et suivent un processus de marche aléatoire appelé mouvement Brownien, voir Fig. 65.

Show code cell source Hide code cell source

"""Brownian motion
code adapted from Scipy Cookbook https://scipy-cookbook.readthedocs.io/items/BrownianMotion.html
under an MIT-like license https://github.com/scipy/scipy-cookbook/blob/master/LICENSE.txt
"""
def brownian(x0, n, dt, delta, out=None):
    """
    Generate an instance of Brownian motion (i.e. the Wiener process):

        X(t) = X(0) + N(0, delta**2 * t; 0, t)

    where N(a,b; t0, t1) is a normally distributed random variable with mean a and
    variance b.  The parameters t0 and t1 make explicit the statistical
    independence of N on different time intervals; that is, if [t0, t1) and
    [t2, t3) are disjoint intervals, then N(a, b; t0, t1) and N(a, b; t2, t3)
    are independent.

    Written as an iteration scheme,

        X(t + dt) = X(t) + N(0, delta**2 * dt; t, t+dt)


    If `x0` is an array (or array-like), each value in `x0` is treated as
    an initial condition, and the value returned is a numpy array with one
    more dimension than `x0`.

    Arguments
    ---------
    x0 : float or numpy array (or something that can be converted to a numpy array
         using numpy.asarray(x0)).
        The initial condition(s) (i.e. position(s)) of the Brownian motion.
    n : int
        The number of steps to take.
    dt : float
        The time step.
    delta : float
        delta determines the "speed" of the Brownian motion.  The random variable
        of the position at time t, X(t), has a normal distribution whose mean is
        the position at time t=0 and whose variance is delta**2*t.
    out : numpy array or None
        If `out` is not None, it specifies the array in which to put the
        result.  If `out` is None, a new numpy array is created and returned.

    Returns
    -------
    A numpy array of floats with shape `x0.shape + (n,)`.

    Note that the initial value `x0` is not included in the returned array.
    """


    x0 = np.asarray(x0)

    # For each element of x0, generate a sample of n numbers from a
    # normal distribution.
    if len(delta)>1:
        r = np.empty(x0.shape + (n,))
        r[0, :] = norm.rvs(size=(n,), scale=delta[0] * sqrt(dt))
        r[1, :] = norm.rvs(size=(n,), scale=delta[1] * sqrt(dt))
        r[2, :] = norm.rvs(size=(n,), scale=delta[2] * sqrt(dt))
    else:
        r = norm.rvs(size=x0.shape + (n,), scale=delta[0] * sqrt(dt))

    # If `out` was not given, create an output array.
    if out is None:
        out = np.empty(r.shape)

    # This computes the Brownian motion by forming the cumulative sum of
    # the random samples.
    np.cumsum(r, axis=-1, out=out)

    # Add the initial condition.
    out += np.expand_dims(x0, axis=-1)

    return out

import numpy as np
from matplotlib import pyplot as plt
from math import sqrt
from scipy.stats import norm

# The Wiener process parameter.
delta = [0.25]
# Total time.
T = 10.0
# Number of steps.
N = 500
# Time step size
dt = T/N
# Initial values of x.
x = np.empty((2,N+1))
x[:, 0] = 0.0

fig = plt.figure(figsize=(5, 5), dpi=100)
ax = plt.axes()
n_samp = 10
points = np.empty((2, n_samp))
for samp in range(n_samp):
    brownian(x[:,0], N, dt, delta, out=x[:,1:])

    # Plot the 2D trajectory.
    ax.plot(x[0, :], x[1, :])
    points[:, samp] = x[:, -1]

# Mark the start and end points.
ax.plot(x[0,0], x[1,0], 'ro', markersize=12, alpha=0.5)
for samp in range(n_samp):
    ax.plot(points[0, samp], points[1, samp],'bo', markersize=12, alpha=0.5)

# More plot decorations.
plt.title('Mouvement Brownien 2D')
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_xlim([-2.5, 2.5])
ax.set_ylim([-2.5, 2.5])

# Glue the figure
from myst_nb import glue
glue("brownian-fig", fig, display=False)

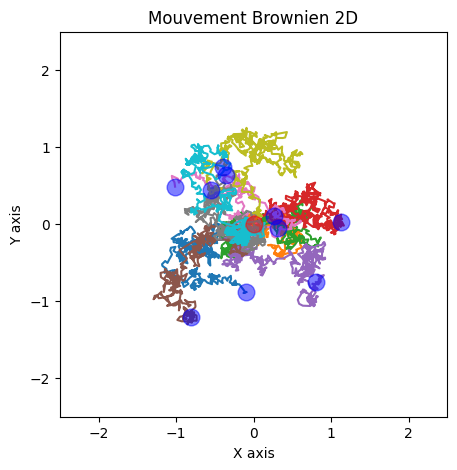
_images/0b2738de9c12a2135b6fd2c5f89d1830a6123054d13eef09237ed63546f74a44.png — Fig. 65 Illustration de mouvement Brownien d’une molécule. Le point de départ est indiqué par un cercle rouge. Les trajectoires de couleurs correspondent à des marches aléatoires simulées suivant un mouvement Brownien. Les points bleus indiquent le point d’arrivée de chaque marche. Figure générée à l’aide de code Python par P. Bellec, sous licence CC-BY 4.0. Le code de simulation de mouvement Brownien est adapté du Scipy Cookbook sous une licence proche de MIT.#

Diffusion isotrope et anisotrope#

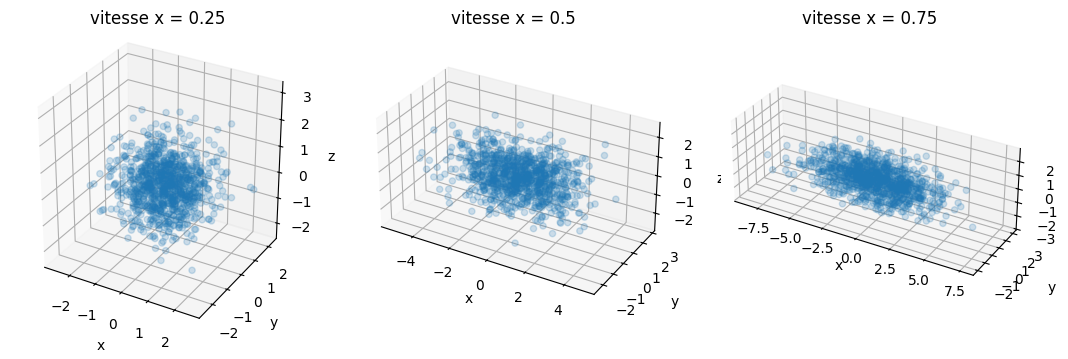
_images/ccde599f4803177110a6084ed1f9cfd5084b6d3f90250aeaf7721138ffa09ca7.png — Fig. 66 Diffusion isotrope vs anisotrope. Chaque rond bleu représente le point d’arrivée d’une molécule d’eau selon une simulation de marche aléatoire avec un processus Brownien en 3D. Sur le graphe de gauche, la vitesse de diffusion des molécules d’eau est identique dans toutes les directions. Sur les graphes du milieu et de droite, la vitesse de diffusion est supérieure selon l’axe `x` que selon `y` et `z`. Figure générée à l’aide de code Python par P. Bellec, sous licence CC-BY 4.0.#

Le déplacement des molécules d’eau dans un milieu suit un mouvement Brownien. Si le milieu a des caractéristiques similaires dans toutes les directions, on parle de milieu isotrope. Le graphe de gauche de la Fig. 66 représente l’ensemble des points d’arrivée de marches aléatoires dans un tel milieu isotrope. On remarque que les molécules se répartissent approximativement dans une sphère. Que se passe-t-il si la diffusion est plus rapide dans une direction donnée, par exemple l’axe x? On parle alors de milieu anisotrope. Sur le graphe du milieu, on voit que la forme remplie par les molécules s’allonge, et ressemble plus à un ballon de football américain qu’à une sphère (ou, en termes mathématiques, une ellipse). Plus la différence de vitesse de diffusion sur x grandit par rapport aux directions y et z, et plus la forme s’allonge (graphe de droite).

Diffusion et fibres de matière blanche#

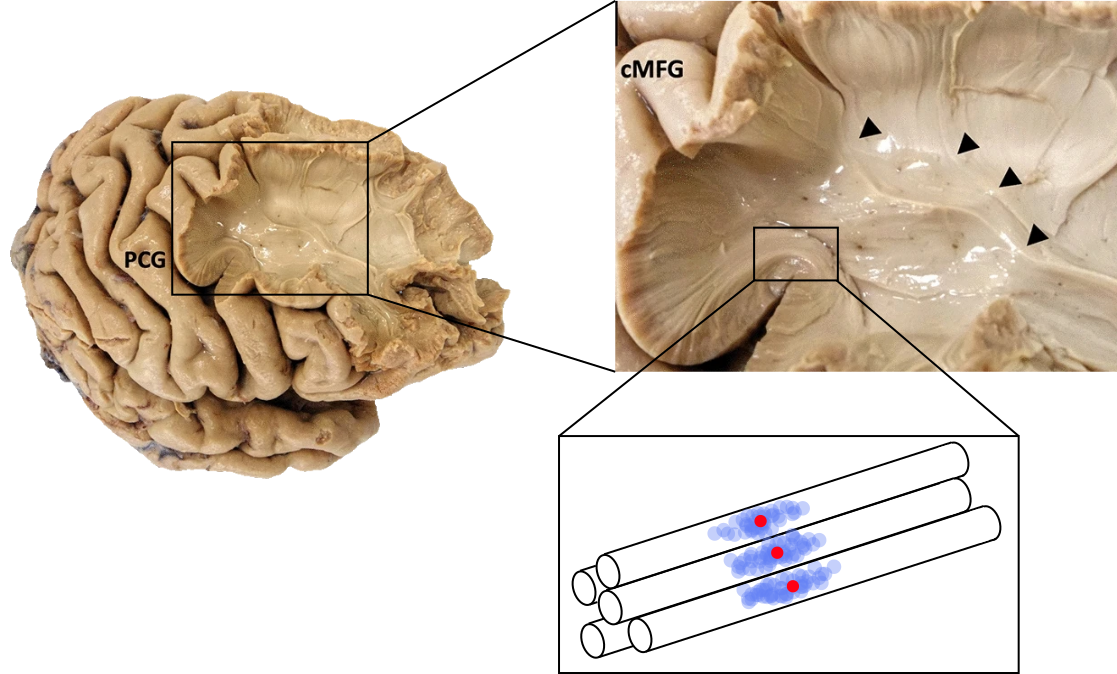
_images/dissection.png — Fig. 67 Dissection cérébrale illustrant l’organisation de la matière blanche cérébrale en faisceaux de fibres. Bas droite: schéma illustrant la diffusion de l’eau contrainte par les fibres. Le point rouge correspond à l’origine de marches aléatoires, dont les terminaisons sont indiquées par les points bleus. Images de cerveau tirées de [29], sous licence CC-BY 4.0. Le reste de la figure par P Bellec, sous licence CC-BY 4.0, inspirée par la thèse de C. Poupon, 1999.#

Les axones des neurones viennent contraindre la diffusion de l’eau, les molécules d’eau ne peuvent donc pas se déplacer librement dans toutes les directions. Le profil de diffusion des molécules d’eau suit alors une forme anisotrope, comme on vient de le voir en Fig. 66. L’eau diffuse plus facilement dans la direction parallèle aux fibres. La diffusion est donc anisotrope et le coefficient de diffusion sera alors plus élevé dans cette direction parallèle, voir Fig. 67. Alors, en sachant comment diffuse l’eau, nous pouvons déterminer la configuration des axones. Le phénomène de diffusion dépend de la structure du tissu! C’est le principe physiologique à l’origine des mesures en IRMd.

Acquisition IRMd#

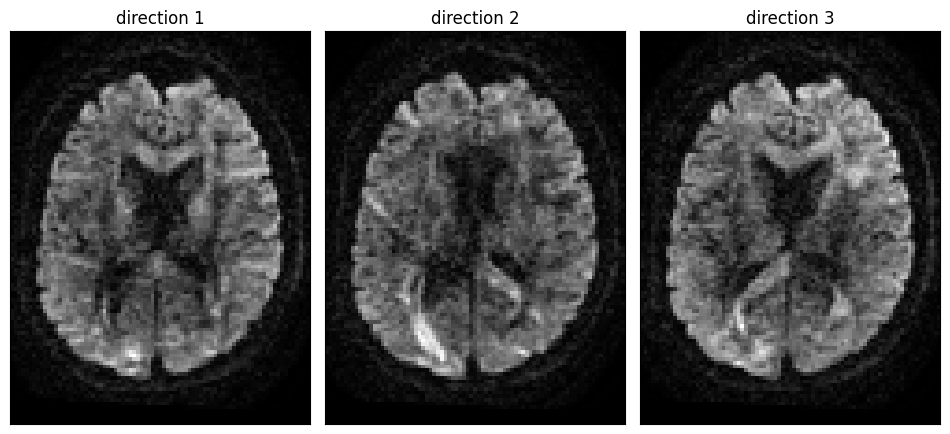
_images/ba57d2936a40aee3cc7d2633df657d2f517236f5cb7c69f7702635e041fe83dd.png — Fig. 68 Volumes IRM pondérées en diffusion. Chaque coupe axiale représente un volume \(T_2\) pondérée en diffusion pour une direction différente. Figure générée à l’aide de code Python par P. Bellec, sous licence CC-BY 4.0. Le code est adapté d’un tutorial de la librairie Dipy, distribuée sous licence BSD 3-Clause.#

En IRM de diffusion, nous allons prendre des images selon plusieurs orientations de gradients. Ce sont des images pondérées en \(T_2\), avec une pondération additionnelle correspondant à la diffusion de l’eau dans une direction correspondant à la direction du gradient appliqué. Pour un voxel donné, nous allons prendre des mesures dans différentes directions de gradients, qui vont nous dire si l’eau a beaucoup diffusé dans cette direction là, un peu comme les points bleus de la Fig. 67. Pour un volume IRMd, la valeur en un voxel nous dit si le point bleu est loin ou pas du point rouge, pour une direction que l’on a sélectionnée, voir Fig. 68

Tenseur de diffusion#

Le modèle du tenseur#

_images/tensor-schematic.png — Fig. 69 La diffusion des molécules d’eau au cours du temps peut se visualiser comme un nuage de points. À cause des contraintes de l’environnement, notamment les axones, ce nuage prend la forme d’un ballon de rugby (haut, gauche). La forme du nuage peut être approximée avec un modèle de tenseur (bas à gauche). Les paramètres principaux de ce modèle sont les directions principales de diffusion \(e_1\), \(e_2\), \(e_3\), ainsi que les valeurs de diffusion associées à ces directions \(\lambda_1 \geq \lambda_2 \geq \lambda_3\). Figure par P. Bellec sous licence CC-BY 4.0, inspirée par M. Descoteaux et C. Poupon,#

À partir des simulations ci-dessus, il est intuitif d’imaginer la diffusion de l’eau comme un ballon, plus ou moins allongé. Mathématiquement, cela se formule avec un tenseur de diffusion, ou modèle Gaussien, voir Fig. 69. Pour estimer la forme du ballon dans chaque voxel, nous utilisons les différentes valeurs de diffusion obtenues pour chaque direction d’acquisition. Si la diffusion est plus grande selon une certaine direction, notre ballon ressemblera plutôt à un ballon de rugby. Si la diffusion est semblable dans toutes les directions d’acquisition, nous obtiendrons plutôt un ballon de soccer.

Imagerie par tenseurs de diffusion#

Show code cell source Hide code cell source

# Import des modules
import numpy as np
from dipy.io.image import load_nifti, save_nifti
from dipy.io.gradients import read_bvals_bvecs
from dipy.core.gradients import gradient_table
import dipy.reconst.dti as dti
from dipy.data import get_fnames

# Select patch
minx = 1
maxx = 81
miny = 1
maxy = 106
minz = 28
maxz = 32

# Télécharge des données HARDI
hardi_fname, hardi_bval_fname, hardi_bvec_fname = get_fnames('stanford_hardi')
data, affine = load_nifti(hardi_fname)
bvals, bvecs = read_bvals_bvecs(hardi_bval_fname, hardi_bvec_fname)
gtab = gradient_table(bvals, bvecs)

# Force affine to something simple to make it easier to extract patches
affine = np.eye(4)

# Masque les données et estime les tenseurs
from dipy.segment.mask import median_otsu
data = data[:, :, minz:maxz, :]
maskdata, mask = median_otsu(data, vol_idx=range(10, 50), median_radius=3,
                             numpass=1, autocrop=True, dilate=2)
tenmodel = dti.TensorModel(gtab)
tenfit = tenmodel.fit(maskdata)

# Génère métriques dérivées (FA etc)
from dipy.reconst.dti import fractional_anisotropy, color_fa
FA = fractional_anisotropy(tenfit.evals)
FA[np.isnan(FA)] = 0
FA = np.clip(FA, 0, 1)
RGB = color_fa(FA, tenfit.evecs)
MD1 = dti.mean_diffusivity(tenfit.evals)

# Figure
from dipy.data import get_sphere
sphere = get_sphere('repulsion724')
from dipy.viz import window, actor
scene = window.Scene()
evals = tenfit.evals[minx:maxx, miny:maxy, :]
evecs = tenfit.evecs[minx:maxx, miny:maxy, :]

# boost the colors
RGB *= 2
RGB[RGB>1] = 1
cfa = RGB[minx:maxx, miny:maxy, :]
scene.add(actor.tensor_slicer(evals, evecs, scalar_colors=cfa, sphere=sphere,
                              scale=0.3))
scene.set_camera(position=(14.87946710578175, 25.770232149765413, 173.54578028650144),
                 focal_point=(33.43851200470716, 40.67356830562871, 15.545914873824975),
                 view_up=(0.003256400517440014, 0.9955397521536979, 0.09428678453221151))
window.record(scene, n_frames=1, out_path='tensor-slice.png',
              size=(1000, 1000), reset_camera=False)
scene.set_camera(position=(6.398539759431944, 36.122368120824724, 21.074961978614017),
                 focal_point=(17.02336666201742, 55.39317316617157, 7.230217513090364),
                 view_up=(0.10205867972271891, 0.5426923506538308, 0.8337080055001721))
window.record(scene, n_frames=1, out_path='tensor-zoom.png',
              size=(600, 600), reset_camera=False)             

# Make figure
from matplotlib import pyplot as plt
import imageio
fig1, ax = plt.subplots(1, 2, figsize=(12, 6), dpi=200,
                        subplot_kw={'xticks': [], 'yticks': []})
fig1.subplots_adjust(hspace=0.3, wspace=0.05)
im = imageio.imread('tensor-slice.png')
ax.flat[0].imshow(im, interpolation='antialiased')
ax.flat[0].set_title('full slice')
im = imageio.imread('tensor-zoom.png')
ax.flat[1].imshow(im, interpolation='none')
ax.flat[1].set_title('zoom')

# Glue the figure
from myst_nb import glue
glue("tensor-fig", fig1, display=False)

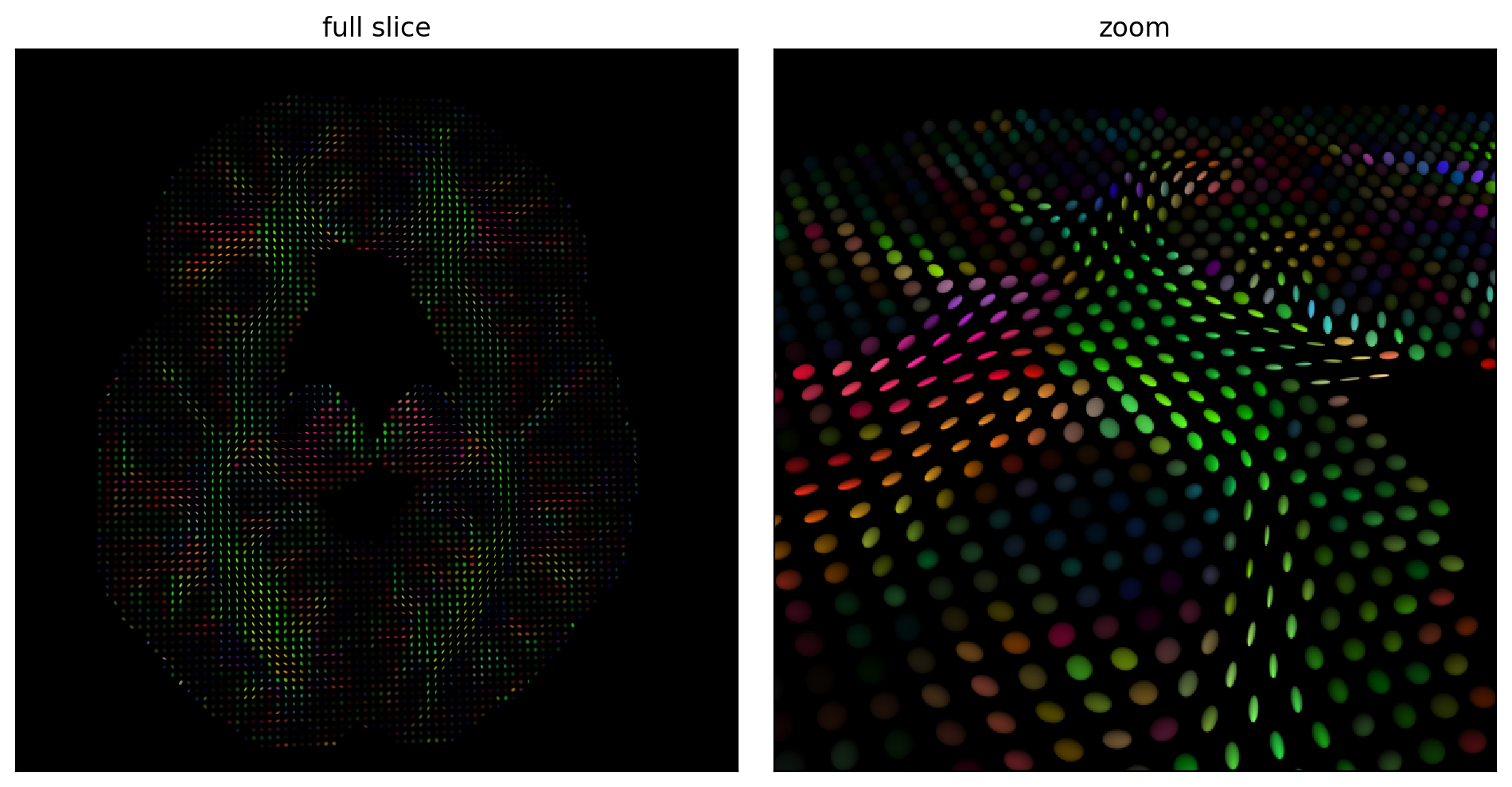
_images/27c2cd3924e91c72647363211d2b7f86d7564b7ac1e4db5db14adcff47d22143.png — Fig. 70 Tenseurs de diffusion estimés sur une coupe axiale (gauche) et zoom sur une portion de la coupe (droite). La couleur de chaque tenseur code pour la direction principale de diffusion, ainsi que l’anisotropie fractionnelle de chaque tenseur. Les tenseurs les plus brillants sont fortement anisotropes, c’est-à-dire que la direction principale de diffusion est nettement plus forte que les directions transverses. Figure générée par du code python adapté d’un tutoriel Dipy par P. Bellec sous licence CC-BY 4.0.#

L’imagerie par tenseurs de diffusion (diffusion tensor imaging, DTI) est l’une des premières techniques d’analyse qui a vu le jour en IRM de diffusion. Pour estimer la forme de notre ballon, nous avons besoin d’au moins six directions d’acquisition: xy, xz, yz, -xy, -xz, y-z. C’est en combinant les images dans ces six directions que nous pouvons estimer notre tenseur de diffusion (notre ballon). Comme nous avons ces mesures pour chacun des voxels, nous pouvons créer un volume cérébral où la valeur de chaque voxel est un tenseur (ballon), voir Fig. 70.

Caractéristiques des tenseurs#

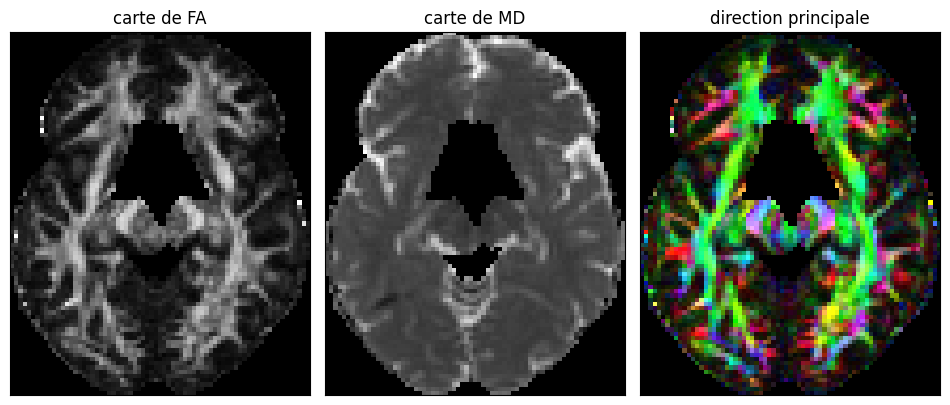
_images/fd0d4877d03c1f7e5c963441e821bae598a7196b5d83ac10465acaf2fbe3e568.png — Fig. 71 Cartes dérivées de tenseurs en IRM de diffusion: anisotropie fractionnelle (gauche), diffusivité moyenne (milieu) et direction principale du tenseur (droite). Pour la direction principale, l’axe médial-latéral (`x`) est codé en rouge, l’axe antérieur-postérieur (`y`) est codé en vert, et l’axe ventral-dorsal (`z`) est codé en bleu. Figure générée à l’aide de code Python adapté d’un tutoriel Dipy par P. Bellec, sous licence CC-BY 4.0.#

Il est possible de résumer certaines caractéristiques importantes des tenseurs de diffusion à l’aide d’une unique mesure, comme l’anisotropie fractionnelle et la diffusivité moyenne (voir définitions ci-dessous). On extrait donc une mesure par voxel, ce qui peut se représenter avec une carte cérébrale, voir Fig. 71. Il est aussi possible de créer une image en couleurs, qui code pour la direction principale de diffusion.

Anisotropie fractionnelle

Une mesure populaire est l’anisotropie fractionnelle (FA en anglais), qui permet de mesurer le degré d’anisotropie d’un phénomène de diffusion, en prenant des valeurs entre 0 et 1. Une valeur d’anisotropie fractionnelle de 0 indique une diffusion isotrope (ballon de soccer), alors qu’une valeur de 1 indique une diffusion fortement anisotropie (ballon de rugby). Par exemple, l’anisotropie fractionnelle de l’eau mesuré dans une bouteille, sans structure, est 0. Les valeurs fortes de FA se retrouvent généralement dans la matière blanche.

Diffusivité moyenne

Nous pouvons aussi mesurer la diffusivité moyenne selon l’équation suivante (voir Fig. 69 pour les notations): \(\overline{\lambda} = \frac{\lambda_{1}+\lambda_{2}+\lambda_{3}}{3}\) La diffusivité moyenne nous indique à quel point il y a de la diffusion à l’intérieur d’un voxel. La diffusivité moyenne est très forte dans le liquide céphalo-rachidien, où les molécules d’eau sont très peu contraintes.

Direction principale de diffusion

Afin de visualiser dans quelle direction principale pointe les tenseurs, une approche populaire consiste à coder chaque axe x, y et z avec une couleur (rouge, vert, bleu, respectivement). Pour une direction donnée, on mélange les trois couleurs dans une proportion correspondant aux contributions des trois axes.

Tractographie#

Tractographie streamline#

Show code cell source Hide code cell source

from dipy.tracking import utils

seeds = utils.seeds_from_mask(mask_wm[minx:maxx, miny:maxy, :], affine, density=[1, 1, 1])

from dipy.tracking.stopping_criterion import ThresholdStoppingCriterion

stopping_criterion = ThresholdStoppingCriterion(FA, 0.1)

from dipy.direction import peaks_from_model
csa_peaks = peaks_from_model(tenmodel, maskdata[minx:maxx, miny:maxy, :, :], sphere,
                             relative_peak_threshold=.8,
                             min_separation_angle=45,
                             mask=mask_wm[minx:maxx, miny:maxy, :])

from dipy.tracking.local_tracking import LocalTracking
from dipy.tracking.streamline import Streamlines

# Initialization of LocalTracking. The computation happens in the next step.
streamlines_generator = LocalTracking(csa_peaks, stopping_criterion, seeds,
                                      affine=affine, step_size=0.2, max_cross=2)
# Generate streamlines object
streamlines = Streamlines(streamlines_generator)

from dipy.viz import colormap
color = colormap.line_colors(streamlines)
streamlines_actor = actor.line(streamlines,
                               colormap.line_colors(streamlines))

# Create the 3D display.
scene = window.Scene()
scene.add(streamlines_actor)
scene.add(actor.tensor_slicer(evals, evecs, scalar_colors=cfa, sphere=sphere,
                              scale=0.3))
scene.set_camera(position=(14.87946710578175, 25.770232149765413, 173.54578028650144),
                 focal_point=(33.43851200470716, 40.67356830562871, 15.545914873824975),
                 view_up=(0.003256400517440014, 0.9955397521536979, 0.09428678453221151))
window.record(scene, n_frames=1, out_path='irm_diffusion/fibers-slice.png',
              size=(1000, 1000), reset_camera=False)
scene.set_camera(position=(6.398539759431944, 36.122368120824724, 21.074961978614017),
                 focal_point=(17.02336666201742, 55.39317316617157, 7.230217513090364),
                 view_up=(0.10205867972271891, 0.5426923506538308, 0.8337080055001721))
window.record(scene, n_frames=1, out_path='irm_diffusion/fibers-zoom.png',
              size=(1000, 1000), reset_camera=False)

# Make figure
from matplotlib import pyplot as plt
import imageio
fig1, ax = plt.subplots(1, 2, figsize=(12, 6), dpi=300,
                        subplot_kw={'xticks': [], 'yticks': []})
fig1.subplots_adjust(hspace=0.3, wspace=0.05)
im = imageio.imread('irm_diffusion/fibers-slice.png')
ax.flat[0].imshow(im, interpolation='antialiased')
ax.flat[0].set_title('full slice')
im = imageio.imread('irm_diffusion/fibers-zoom.png')
ax.flat[1].imshow(im, interpolation='antialiased')
ax.flat[1].set_title('zoom')

# Glue the figure
from myst_nb import glue
glue("fibers-fig", fig1, display=False)

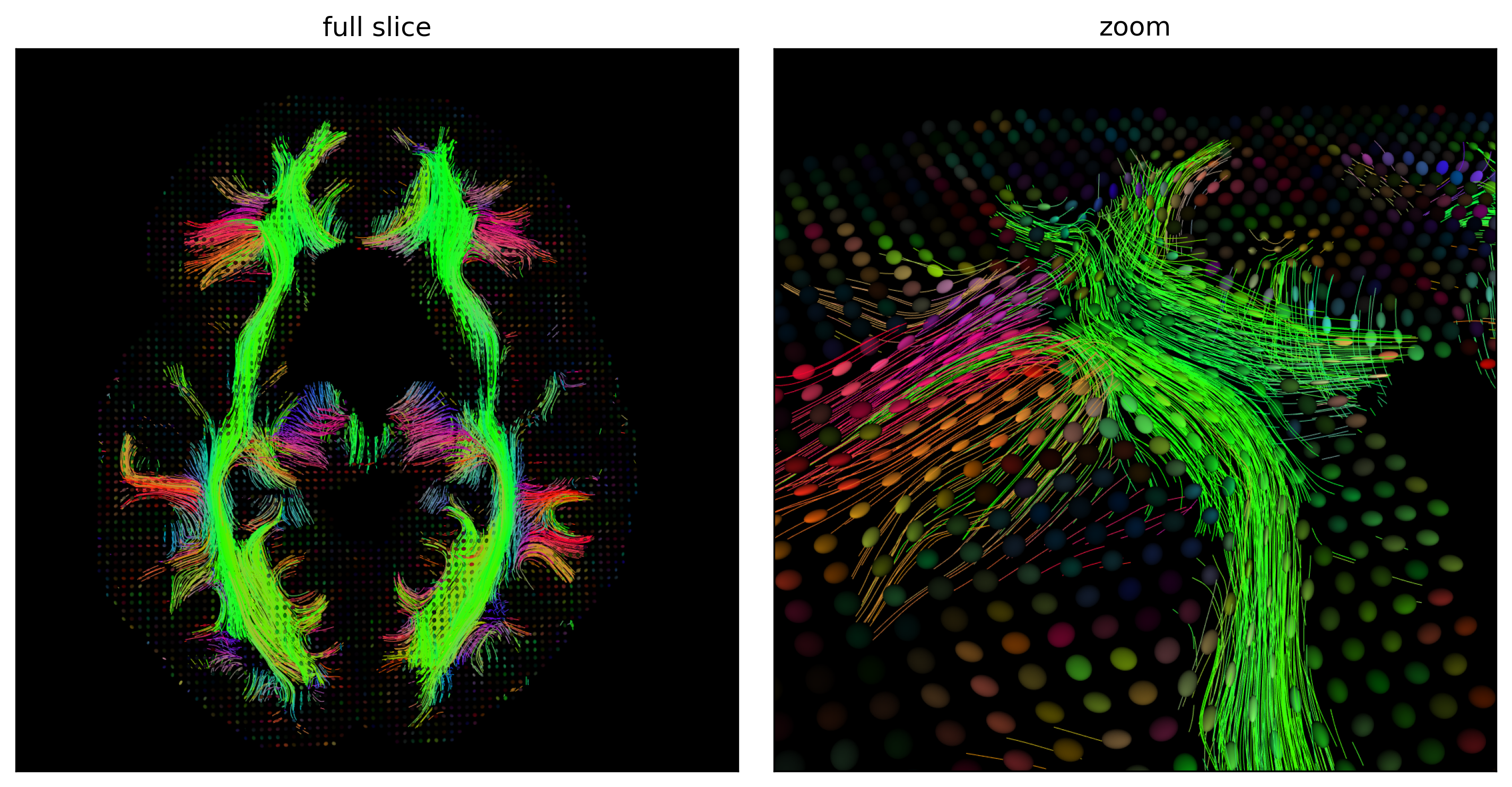
_images/85a7670f5ce30c9bc88b210708d5e09093b870517000b93da38046ede1c9f4ea.png — Fig. 72 Fibres reconstruites par une approche streamline déterministe, qui consiste à tracer une fibre en suivant la direction principale de chaque tenseur de manière itérative, à partir de l’ensemble des points dans la matière blanche sur une coupe axiale (gauche) et zoom sur une portion de la coupe (droite). La couleur de chaque fibre code pour la direction principale de diffusion le long de la fibre. Figure générée par du code python adapté d’un tutoriel Dipy par P. Bellec sous licence CC-BY 4.0.#

La tractographie permet de tracer le chemin des fibres de matière blanche in vivo. Il existe plusieurs approches de tractographie. La tractographie streamline déterministe permet de reconstruire les fibres de matière blanche en partant d’un point donné dans la matière grise et en se déplaçant de manière itérative selon la direction principale de diffusion. Le chemin va se terminer lorsque nous arrivons dans la matière grise. Ce chemin va être tracé grâce à un logiciel. La tractographie probabiliste est similaire à la tractographie déterministe, mais considère en plus une incertitude sur la direction des fibres de matière blanche. Donc au lieu de reconstruire une seule fibre associée à un point de la matière blanche, la tractographie probabiliste va en reconstruire plusieurs qui seront toutes légèrement différentes.

Étapes de prétraitement

Tout comme l’IRMf des étapes de recalage et de débruitage sont nécessaires pour préparer les données avant d’estimer les tenseurs et effectuer la tractographie. De nombreux paramètres sont à sélectionner pour la tractographie elle-même, qui peuvent influencer les résultats. Il est aussi nécessaire de sélectionner un masque de la matière blanche qui contient les points de départ pour la reconstruction de fibres, obtenu ici par seuillage d’une carte de FA.

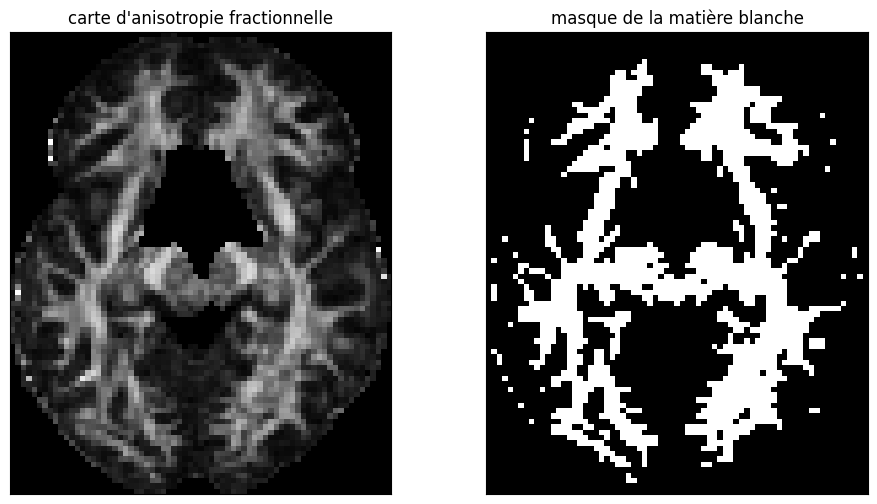
_images/999e3bbfda1ceb7e2a2d107493cf7897d74edb9099f21aac4d2c1ec78dfaa78a.png — Fig. 73 Carte d’anisotropite fractionnelle (gauche) et masque de la matière blanche obtenue par seuillage (droite). Figure générée par du code python adapté d’un tutoriel Dipy par P. Bellec sous licence CC-BY 4.0.#

Croisement de fibres#

_images/crossing-fibers.png — Fig. 74 Illustration du problème de croisement de fibres, illustré à gauche. La diffusion de l’eau dans chaque fibre est associée à un tenseur qui pointe dans une direction différente (milieu). Lorsqu’on essaye d’approximer la diffusion dans le croisement avec un seul tenseur, on observe un tenseur isotrope (droite). Figure par P Bellec, sous licence CC-BY 4.0, inspiré par la thèse de C. Poupon, 1999.#

Une limitation que nous rencontrons avec l’imagerie en tenseur de diffusion est le croisement de fibres. Il est très courant dans la matière blanche d’avoir plusieurs faisceaux de fibres qui se croisent. Lorsque beaucoup de fibres se croisent comme dans la figure ci-dessous, le tenseur de diffusion apparaît isotrope, même s’il y a effectivement des fibres présentes dans le voxel. Dans ce cas, l’algorithme de reconstruction de fibres ne saura pas quelle direction suivre. Une des technique utilisée pour résoudre ce problème est l’imagerie de diffusion à haute résolution, qui nous permet d’estimer plusieurs tenseurs pour un même voxel. Cette technique consiste à effectuer l’acquisition des données sur de nombreuses directions (une trentaine à une soixantaine de directions) en utilisant une séquence HARDI (High Angular Resolution Diffusion Imaging). Les acquisitions réalisées avec cette séquence sont plus longues que celles en DTI, 5-30 min vs 3-4 min.

Show code cell source Hide code cell source

from matplotlib import pyplot as plt
from dipy.reconst.csdeconv import auto_response_ssst
from dipy.reconst.csdeconv import ConstrainedSphericalDeconvModel
from dipy.data import default_sphere
response, ratio = auto_response_ssst(gtab, maskdata, roi_radii=10, fa_thr=0.7)
csd_model = ConstrainedSphericalDeconvModel(gtab, response)
csd_fit = csd_model.fit(maskdata)
csd_odf = csd_fit.odf(default_sphere)
from dipy.data import default_sphere
fodf_spheres = actor.odf_slicer(csd_odf, sphere=default_sphere, scale=0.9,
                                norm=False, colormap='plasma')

# Create the 3D display.
scene = window.Scene()
scene.add(fodf_spheres)
scene.set_camera(position=(14.87946710578175, 25.770232149765413, 173.54578028650144),
                 focal_point=(33.43851200470716, 40.67356830562871, 15.545914873824975),
                 view_up=(0.003256400517440014, 0.9955397521536979, 0.09428678453221151))
window.record(scene, n_frames=1, out_path='irm_diffusion/fodf-slice.png',
              size=(1000, 1000), reset_camera=False)
scene.set_camera(position=(6.398539759431944, 36.122368120824724, 21.074961978614017),
                 focal_point=(17.02336666201742, 55.39317316617157, 7.230217513090364),
                 view_up=(0.10205867972271891, 0.5426923506538308, 0.8337080055001721))
window.record(scene, n_frames=1, out_path='irm_diffusion/fodf-zoom.png',
              size=(600, 600), reset_camera=False)   

# Make figure
from matplotlib import pyplot as plt
import imageio
fig1, ax = plt.subplots(1, 2, figsize=(12, 6), dpi=200,
                        subplot_kw={'xticks': [], 'yticks': []})
fig1.subplots_adjust(hspace=0.3, wspace=0.05)
im = imageio.imread('irm_diffusion/fodf-slice.png')
ax.flat[0].imshow(im, interpolation='antialiased')
ax.flat[0].set_title('full slice')
im = imageio.imread('irm_diffusion/fodf-zoom.png')
ax.flat[1].imshow(im, interpolation='none')
ax.flat[1].set_title('zoom')

# Glue the figure
from myst_nb import glue
glue("fodf-fig", fig1, display=False)

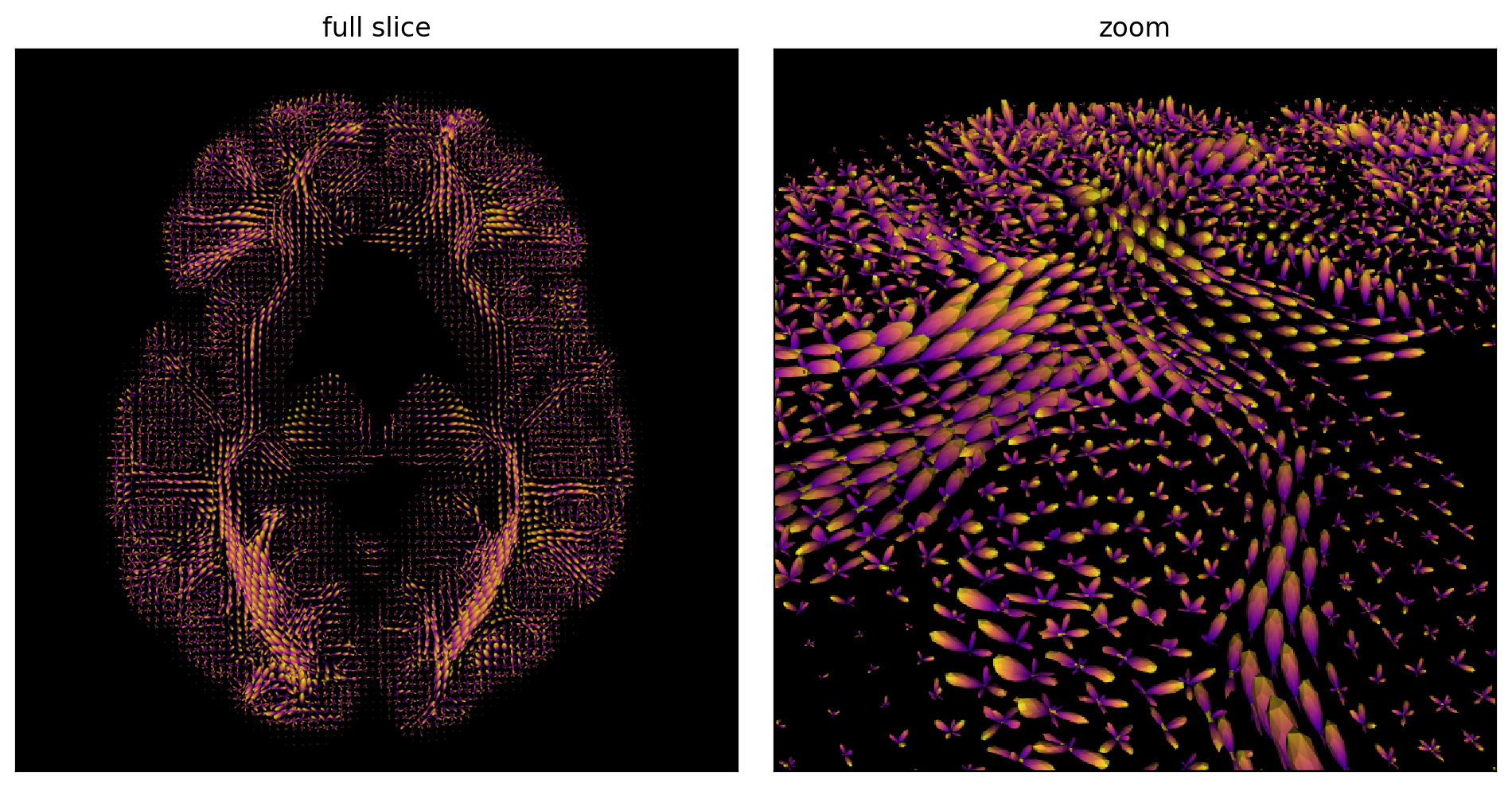
_images/4ff8454ea76f53f8fd6e26aca17f2e0b0e3e09c85695e6aa12985f06e61db6b6.png — Fig. 75 Estimation de fODF sur une coupe axiale (gauche) et zoom sur une portion de la coupe (droite). Figure générée par du code python adapté d’un tutoriel Dipy par P. Bellec sous licence CC-BY 4.0.#

Avec une séquence HARDI, nous pouvons estimer une fonction de distribution des orientations de fibres (fiber Orientation Distribution Function, fODF) lorsqu’il y a des croisements de fibres perpendiculaires. Ceci nous permet d’estimer plusieurs tenseurs à l’intérieur d’un voxel et de surpasser certaines limites du tenseur de diffusion (DTI). Dans les zones à faible anisotropie nous observons plusieurs directions, comme des petits ballons dans chaque voxel, alors que nous observons une direction principale dans les fibres les plus importantes.

Show code cell source Hide code cell source

csa_peaks = peaks_from_model(csd_model, maskdata[minx:maxx, miny:maxy, :, :], default_sphere,
                             relative_peak_threshold=.5,
                             min_separation_angle=15,
                             mask=mask_wm[minx:maxx, miny:maxy, :])

# Initialization of LocalTracking. The computation happens in the next step.
streamlines_generator = LocalTracking(csa_peaks, stopping_criterion, seeds,
                                      affine=affine, step_size=0.2, max_cross=5)
# Generate streamlines object
streamlines = Streamlines(streamlines_generator)

from dipy.viz import colormap
color = colormap.line_colors(streamlines)
streamlines_actor = actor.line(streamlines,
                               colormap.line_colors(streamlines))

# Create the 3D display.
scene = window.Scene()
scene.add(streamlines_actor)
scene.add(fodf_spheres)
scene.set_camera(position=(14.87946710578175, 25.770232149765413, 173.54578028650144),
                 focal_point=(33.43851200470716, 40.67356830562871, 15.545914873824975),
                 view_up=(0.003256400517440014, 0.9955397521536979, 0.09428678453221151))
window.record(scene, n_frames=1, out_path='fibers-slice.png',
              size=(1000, 1000), reset_camera=False)
scene.set_camera(position=(6.398539759431944, 36.122368120824724, 21.074961978614017),
                 focal_point=(17.02336666201742, 55.39317316617157, 7.230217513090364),
                 view_up=(0.10205867972271891, 0.5426923506538308, 0.8337080055001721))
window.record(scene, n_frames=1, out_path='fibers-zoom.png',
              size=(1000, 1000), reset_camera=False)

# Make figure
from matplotlib import pyplot as plt
import imageio
fig1, ax = plt.subplots(1, 2, figsize=(12, 6), dpi=300,
                        subplot_kw={'xticks': [], 'yticks': []})
fig1.subplots_adjust(hspace=0.3, wspace=0.05)
im = imageio.imread('fibers-slice.png')
ax.flat[0].imshow(im, interpolation='antialiased')
ax.flat[0].set_title('full slice')
im = imageio.imread('fibers-zoom.png')
ax.flat[1].imshow(im, interpolation='antialiased')
ax.flat[1].set_title('zoom')

# Glue the figure
from myst_nb import glue
glue("fodf-tracts-fig", fig1, display=False)

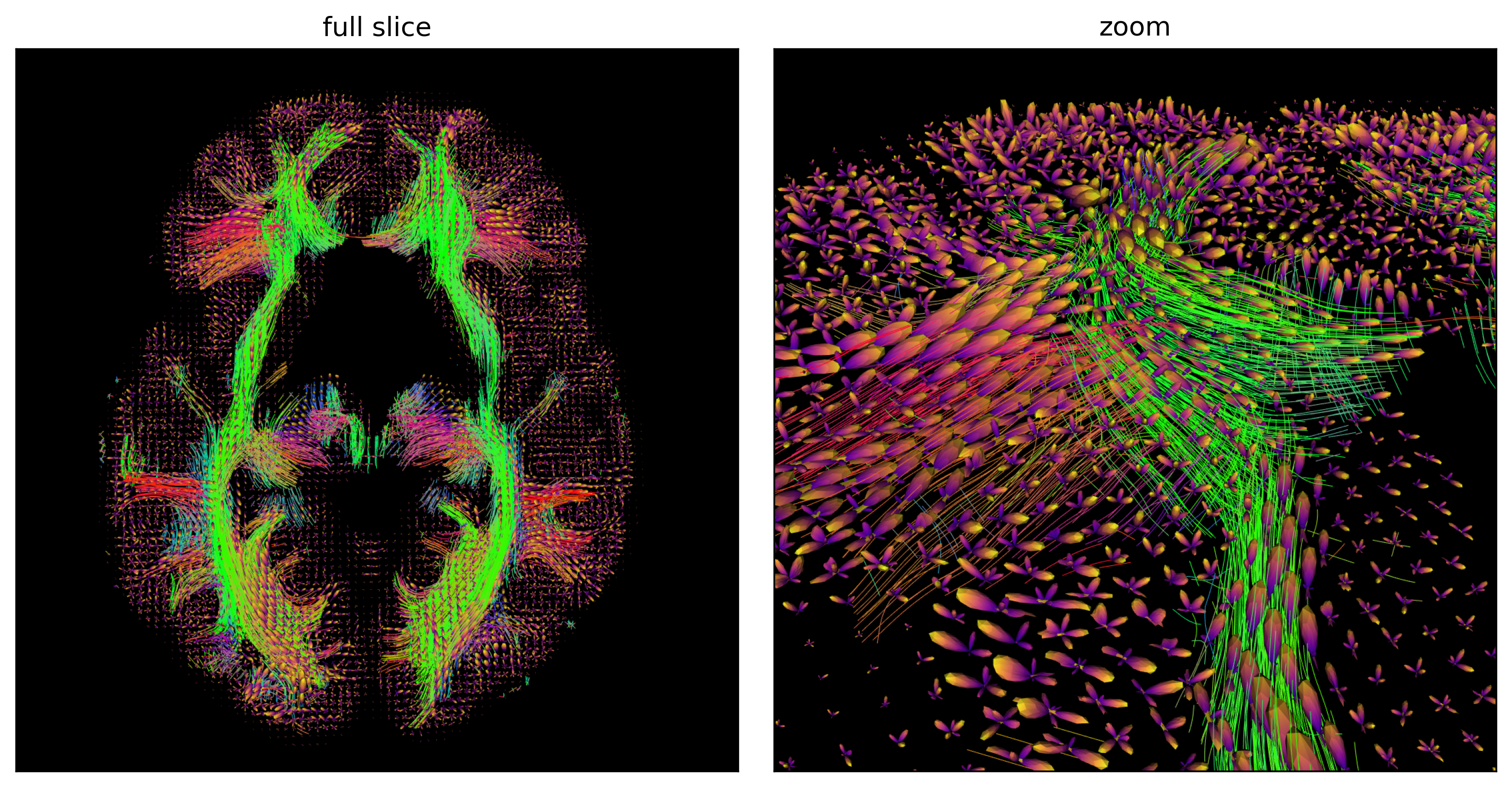
_images/6f3c4056c244749a5068981db41c638799e295884e475ec9118818af59b93d6c.png — Fig. 76 Fibres reconstruites par une approche streamline déterministe avec une approche multi-tenseurs, qui permet de suivre plusieurs pics de diffusion à chaque voxel, à partir de l’ensemble des points dans la matière blanche sur une coupe axiale (gauche) et zoom sur une portion de la coupe (droite). Cette approche permet d’être plus robuste à la présence de croisement de fibres. Figure générée par du code python adapté d’un tutoriel Dipy par P. Bellec sous licence CC-BY 4.0.#

La capacité de fODF de représenter plusieurs tenseurs à chaque voxel permet de reconstruire des fibres qui se croisent, comme il est apparent dans le zoom de la Fig. 76. Il est important de réaliser que les données utilisées pour générer Fig. 72 et Fig. 76 sont les mêmes, mais les fibres reconstruites sont très différentes! Les paramètres que l’on choisit pour la méthode de reconstruction vont aussi changer la forme et le nombre de fibres. La tractographie en IRMd n’est donc pas une science exacte, et les faux positifs (une fibre reconstruite qui n’existe pas vraiment) ainsi que les faux négatifs (une fibre que l’on ne reconstruit pas mais qui existe pourtant) sont très courants.

Faisceaux de fibres#

_images/faisceaux.png — Fig. 77 Illustration de trois faisceaux de fibres: les radiations optiques (OR), le faisceau arquée (AF) et le faisceau occipital vertical (VOF). Les faisceaux sont présentés sur différentes vues d’une dissection (A, B, D), ainsi qu’à l’aide d’une dissection virtuelle (C). Figure tirées de [30], sous licence CC-BY 4.0.#

Nous pouvons fournir aux algorithmes de tractographie des a priori sur les fibres dans le cerveau que nous connaissons à partir des études de dissection. Dans une reconstruction systématique des fibres, tout va être tracé, alors que dans une dissection virtuelle, seuls certains paquets de fibres vont être sélectionnés. Ces a priori permettent de limiter les faux positifs, et l’utilisation d’algorithmes de tractographie performants permet de limiter les faux négatifs. Il existe un certain nombre de faisceaux de fibres classiques avec des schémas de dissection bien établis, comme le corps calleux, le faisceau arqué, ou bien le fascicule longitudinal supérieur.

Il est possible de calculer la valeur moyenne de l’anisotropie fractionnelle, ou tout autre métrique, le long d’une fibre. Cette approche est appellée tractométrie: on effectue une série de mesures le long d’une fibre. La fibre peut également être découpée en segments, pour améliorer la précision spatiale de la mesure. On peut ensuite comparer ces valeurs entre différents individus pour faire des tests statistiques. Dans ce cas, le recalage entre individus se fait via l’identification de faisceaux de fibres, plutôt que par une méthode de déformation non-linéaire.

Conclusion#

Dans ce cours, nous avons vu les principes de l’IRM de diffusion. Plus précisément, nous avons vu:

Comment obtenir des images en IRMd grâce à la diffusion de l’eau dans différentes directions
Comment estimer le processus de diffusion à l’aide de tenseurs et d’en mesurer différentes métriques (diffusivité moyenne, anisotropie fractionnelle)
Le principe des méthodes de tractographie.
Comment estimer les croisements de fibres.
Comment l’IRMd peut être utilisée pour effectuer une dissection virtuelle.

Exercices#

Exercice 1

Vrai/faux. Les images générées par le scanner en IRM de diffusion sont…

Une image avec un tenseur à chaque voxel.
Une image avec un ou plusieurs tenseurs à chaque voxel.
Une série d’images sensibles à la diffusion de l’eau dans différentes directions.
Des images où l’on voit les fibres de matière blanche du cerveau en 3D.

Exercice 2

Anisotropie fractionnelle et diffusivité moyenne: vrai-faux.

Le liquide céphalo-rachidien a une faible anisotropie fractionnelle, avec une forte diffusivité moyenne.
Le corps calleux a une très forte diffusivité moyenne.
Une zone avec de nombreux croisements de fibres peut avoir une faible anisotropie fractionnelle.
Le corps calleux a une faible anisotropie fractionnelle.

Exercice 3

Choisissez la bonne réponse. On dispose de données d’IRM de diffusion à haute résolution HARDI:

On peut générer une carte avec un tenseur de diffusion par voxel.
On peut générer une carte avec plusieurs tenseurs de diffusion par voxel.
On doit utiliser plusieurs tenseurs de diffusion par voxel pour reconstruire des fibres.
Réponses 1 et 2.
Réponses 1, 2 et 3.

Exercice 4

Choisissez la bonne réponse. Les fibres reconstruites en IRM de diffusion…

Peuvent manquer des fibres existantes, à cause notamment du “fiber kissing”, ou des fibres qui n’existent pas, à cause notamment des croisements de fibres.
Reflètent l’ensemble des axones dans le cerveau.
Dépendent à la fois du type de données recueillies et de l’algorithme utilisé.
Réponses 1 et 2.
Réponses 1, 2 et 3.

Exercice 5

Une chercheuse souhaite reconstruire le faisceau longitudinal supérieur au niveau individuel, à l’aide de données d’IRM de diffusion. La méthode utilisée est une tractographie “streamline” déterministe. Citez deux exemples de problèmes qui peuvent faire échouer cette approche. Expliquer comment la chercheuse peut limiter ces problèmes.

Exercice 6

On s’intéresse au faisceau arqué chez un patient qui a une tumeur au cerveau. On réalise un examen en IRM de diffusion à haute résolution. Pensez vous qu’on puisse réaliser une tractographie virtuelle de ce faisceau? Quel aspect de la méthode devra potentiellement être modifié pour prendre en compte pour accommoder la présence de la tumeur? Justifiez vos réponses.

Exercice 7

Pour répondre aux questions de cet exercice, lisez d’abord l’article Quantification of apparent axon density and orientation dispersion in the white matter of youth born with congenital heart disease de Easson et collaborateurs (publié en 2020 dans la revue Neuroimage, volume 205, ID 116255). Celui-ci est disponible en libre accès à cette adresse. Les questions suivantes requièrent des réponses à développement court.

Quelle technique de neuroimagerie est utilisée? S’agit-il d’une technique structurelle ou fonctionnelle?
Quelle type de séquence d’acquisition d’image est utilisé? Listez les paramètres.
Quelle technique de tractographie a été appliquée?
Quelle techniques de tractométrie ont été appliquées?
Quel est le résultat principal de l’étude?

IRM de diffusion

Contents

IRM de diffusion#

Objectifs du cours#

Principes physiques et physiologiques#

Diffusion de l’eau#

Diffusion isotrope et anisotrope#

Diffusion et fibres de matière blanche#

Acquisition IRMd#

Tenseur de diffusion#

Le modèle du tenseur#

Imagerie par tenseurs de diffusion#

Caractéristiques des tenseurs#

Tractographie#

Tractographie streamline#

Croisement de fibres#

Faisceaux de fibres#

Conclusion#

Exercices#